Adventskalender Lösungen

Adventskalender 2013

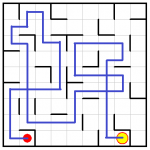
Lösung zum 1.12.
Die Spielidee wird auch unter dem Namen „Vexed-Puzzle“ in verschiedenen Programmen angeboten.
Die Schwierigkeit besteht nur darin, die ungeradzahlig vielen Pakete so zu platzieren, dass sie teleportiert werden. Hier ist eine mögliche Zugfolge:
Martok aus der 1.Spalte zweimal nach rechts, Tranx aus der 4.Spalte nach links, Narses hat seine Geschenke, jaenicke aus der 6.Spalte nach links, Tranx aus der 6.Spalte zweimal links, Martok aus der 6.Spalte dreimal links, Horst_H 1.Spalte 2mal links, usw…

Lösung zum 2.12.
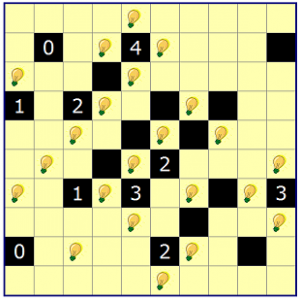
Das Spiel heißt „Akari“.
Man sollte zuerst alle 4 Felder um die „4“ füllen. Die zwei Einzelfelder bei „2“ und „3“ füllen. Bei dieser „3“ können nur noch 2 Felder mit Lampen versehen werden, sonst hat die „2“ zu viele. Die restlichen Felder müssen nun noch abgearbeitet werden. Ist eines nicht beleuchtet, dann wird dort eine zusätzliche Lampe hineingesetzt.
Eine mögliche Lösung wäre:
Sieht das Spielfeld etwas anders, so ist es nur gespiegelt oder gedreht.

Lösung zum 3.12.

1w + 1h + 1f + 1m + 1z + 1o = 1470 1w + 1h – 1f – 1m – 1z – 1o = 230 1w – 1m – 1z – 1o = 0 1h – 1m – 1z = 0 3h -15f + 5z = 0

Dieses ist unterbestimmt und liefert die Lösungen

w = 425 +0,5·e h = 425 -0,5·e f = 195 -0,5·e m = 95 +0,7·e z = 330 -1,2·e o = 1·e

Da m ein Vielfaches von 100 sein soll, kann m nur 100, 200, … werden. Da alle Anteile durch 10 teilbar sein sollen, muss 10(m-95) durch 7 teilbar sein, andernfalls treten Dezimalbrüche auf.
Dies geht nur für m = 200, 900, … Nur für m = 200 ergeben sich für die anderen Zutaten stets positive Werte, d.h. die Lösung ist w = 500 g Weizenmehl ; h = 350 g Honig ; f = 120 g Feinzucker ; m = 200 g Halbfettmargarine ; z = 150 g gewürfeltes Zitronat ; o = 150 g gewürfeltes Orangeat.
Außerdem kann man auch jede Unbekannte durch ihr Zehntel ersetzen (durch 10 teilbar). Dann werden die Zahlen etwas kleiner und handlicher.

Lösung zum 4.12.
Bewegt man die Figur nach rechts, sollte die blaue Kugel so fallen, dass das Monster ziemlich weit unten erlegt wird.
Danach können die blauen Kugeln durch das Gitter geschoben werden/fallen und sich in Diamanten verwandeln. Diese sind einfach einzusammeln. Nach dem der Diamand rechts oben geholt wurde, geht es nach links unten zum Ausgang; ohne vom Monster erledigt zu werden.

Lösung zum 5.12.
Das Alter der drei Kinder soll als ganzzahlig angenommen werden. Es gibt 8 verschiedene Möglichkeiten, aus einem Produkt von drei natürlichen Zahlen als Ergebnis 36 zu erhalten. Die folgende Tabelle zeigt diese Produkte zusammen mit der Summe:
1 · 1 · 36 = 36; Summe: 38
1 · 2 · 18 = 36; Summe: 21
1 · 3 · 12 = 36; Summe: 16
1 · 4 · 9 = 36; Summe: 14
1 · 6 · 6 = 36; Summe: 13
2 · 2 · 9 = 36; Summe: 13
2 · 3 · 6 = 36; Summe: 11
3 · 3 · 4 = 36; Summe: 10
Nehmen wir zuerst an, der Nikolaus kennt die Hausnummer: Nur wenn die Summe 13 beträgt, reichen die Informationen noch nicht zur Lösung aus; das Ergebnis ist dann noch nicht eindeutig. Da es aber ein ältestes Kind geben soll, kommt nur die folgende Lösung in Frage: 9, 2 und 2
Sollte der Nikolaus die Hausnummer aber nicht kennen, genügt die Aussage über das älteste Kind nicht, da es dann noch 7 Möglichkeiten gibt. Da er nicht weiterfragt, kennt er also die Hausnummer.

Lösung zum 6.12.
Mit den 4-Stangen-Türme von Hanoi wird die notwendige Zuganzahl 25. Bei 3 Säulen wären es 2^7-1 = 127 Züge.
Die Grundidee besteht darin, die 3 oberen Scheiben von A mit Hilfe der 3 anderen Stangen z.B. nach B zu transportieren. Dann bringt man die nächsten 3 Scheiben von A wie beim 3-Säulen-Spiel nach C.
Die letzte Scheibe von A geht nach D. Danach schafft man die 3 Scheiben von C nach D und die 3 von A nach D.
Eine möglich Zugfolge ist:
A nach C, A nach D, A nach B, D nach B, C nach B, A nach C, A nach D, C nach D, A nach C, D nach A, D nach C, A nach C, A nach D, C nach D, C nach A, D nach A, C nach D, A nach C, A nach D, C nach D, B nach A, B nach C, B nach D, C nach D, A nach D

Lösung zum 7.12.
Für das Sudoku müssen die Ausgangszahlen ermittelt werden. Die korrekten Antworten sind:

• A1 : maximale Augenzahl bei einem Spielwürfel = 6
• A3 : Anzahl regelmäßiger Sternpolyeder = 4
• A4 : Anzahl der griechischen Musen = 9
• A5 : Anzahl der Tore Thebens = 7
• A8 : auf tschechisch „jeden“ = 1
• B3 : Anzahl der Symmetrieachsen eines Rechtecks = 2
• B4 : zweite Dezimalstelle der Eulerschen Zahl = 1
• B5 : Anzahl der Himmelsrichtungen = 4
• B8 : Nenner des vollständig gekürzten Bruchs 112 / 144 = 9
• B9 : Flächeninhalt des Dreiecks mit den Seiten 3, 4 und 5 = 6
• C1 : Anzahl der Weihnachtsmann-Rentiere, ohne Rudolph = 8
• C7 : auf Latein „quattuor“ = 4
• D2 : auf französisch „sept“ = 7
• D4 : vierte Dezimalziffer von Pi = 5
• D5 : Basis der Ternärsystems = 3
• D8 : Periodenlänge des Bruchs 1/7 = 6
• D9 : 984 : 123 = 8
• E1 : ggT von 15 und 35 = 5
• E2 : kleinste Kubikzahl größer 1 = 8
• E5 : Höhe in cm von Altenburger Spielkarten = 9
• E8 : Anzahl der Prüfungen für die Goldmarie = 3
• E9 : Anzahl der Adventswochen = 4
• F1 : 4² – 3² – 2² – 1² = 2
• F6 : Anzahl der Zwerge bei Schneewittchen = 7
• G2 : Anzahl amtierender Weihnachtsmänner = 1
• G4 : im Dualsystem 10000 : 100 = 4
• G6 : Zinsen bei 1,5 % Zinssatz und 200 Grundwert = 3
• G9 : vierte Wurzel von 16 = 2
• H2 : Aschenputtel hatte ??? böse Schwestern = 2
• H3 : Anzahl platonischer Körper = 5
• H6 : Anzahl der Seitenflächen eines Würfels = 6
• H7 : Anzahl der Ankreise eines Dreiecks = 3
• I3 : über soviele „Brücken musst Du gehen“ = 7
• I4 : Basis des Zahlensystems der Na’vi auf Pandora = 8
• I7 : Zähler von 2/5 – 1/3 , gekürzt = 1
• I9 : Ecken einer Seitenfläche eines Dodekaeders = 5

Danach löst man das Sudoku wie gewohnt. Etwas Hilfe bekommt man auch von dem im Programm eingebauten Hilfeschalter. Die Lösung ist:

6 5 4 9 7 2 8 1 3 7 3 2 1 4 8 5 9 6 8 9 1 3 6 5 4 2 7 1 7 9 5 3 4 2 6 8 5 8 6 2 9 1 7 3 4 2 4 3 6 8 7 9 5 1 9 1 8 4 5 3 6 7 2 4 2 5 7 1 6 3 8 9 3 6 7 8 2 9 1 4 5

Lösung zum 8.12.
Die Kodierungsscheibe gehört zur Alberti-Chiffrierung.
An der äußeren Scheibe sucht man den Code-Buchstaben und liest innen ab, d.h. für das erste C wird ein m.
Für den zweiten Buchstaben muss man aber die äußere Scheibe um ein Feld in Uhrzeigerrichtung drehen, so dass aus dem Z ein a wird. Verfährt man so weiter und beachtet, dass innen kein u sondern nur ein v auftritt, ergibt sich als Weisheit mathematiklehrersindavchnvrmenschen

Lösung zum 9.12.
Bezeichnet man die Richtungen mit u für hoch (up), d für runter (down), l für links und r für rechts ist die Zugfolge: urdldluluruldruldrdr

Lösung zum 10.12.
Sokoban-Rätsel sind natürlich Klassiker. Für diese Aufgabe ist die Lösung etwas länger.
Dabei bedeutet 0 nach oben, 1 nach rechts, 2 nach unten und 3 nach links:

101122212332301121110112333333230 1111111122301033333331111112223300 22110003333032123310111210112230 10333333230021111100012221223300 1200012300012333012222333300000 33210122212233012103000001110122 22221233332303012111100032212333 23021011000010033332210301110122 2212223333300022211100001003332 23001111222221233332300000222211 11222300103333230111112222230000 1033311001000033322322221230000 01001112221103223223333000010011 1222221233331110000003332232222 0000100322220003321012200011112 22222222101032301033333111110123 22110332301033331111000122232211 03323010333

Lösung zum 11.12.
Mit dem Hinweis, dass Delphiana sich für die Geschichte des antiken Roms interessiert, war klar, dass nur das Cäsar-Verfahren vorliegen kann. Allerdings sind die Zeichen nicht im 26buchstabigen Alphabet verschoben, sondern über alle Zeichen im ASCII-Satz und zwar um den Wert 7.
Zur Lösung muss der String markiert und kopiert werden. In einem kleinen Programm verschiebt man jedes Zeichen im ASCII-Code um 7 „abwärts“. Es sollte sich

x = 2; y = 5; z = 0; solange x>0 ist, wiederhole {wenn x ungerade dann z = z+y; y = 2·y; x = x div 2} Ausgabe z

ergeben. Der Algorithmus; binäres Multiplizieren, ägyptische Multiplikation, russische Bauernmultiplikation, usw. genannt; berechnet das Produkt a*b, so dass das Ergebnis 10 ist.

Lösung zum 12.12. und 13.12.
Da bei jedem Start eine andere Zahlenpyramide konstruiert wird, gibt es keine eindeutige Lösung.
Auch bei den Farbkreisen kann man keine Lösung angeben.

Lösung vom 14.12.
Eine Zugfolge zum Zusammensetzen von Rudolph kann schlecht angegeben werden.

Lösung vom 15.12.
Das berühmteste Werk über mathematische Spiele, „Cyclopedia of Puzzles“ von Sam Loyd, enthält neben dem Klassiker „Spiel 15“ auch das Puzzle aus der Aufgabe.
Allerdings ist Loyd nicht der Erfinder. Schon 1909 beschrieb L.W.Hardy das Puzzle und ließ es sich patentieren. Er nannte es Dad’s Puzzle. Bis heute wird das Rätsel immer wieder „neuerfunden“ und vertrieben.

Es ist ziemlich schwierig und eine optimale Lösung ist:
1, 2, 3, 5 zwischen 3 und 4, 1, 9, 8, 6, 7, 4, 5, 1, 9, 8, 6, 7, 4 zwischen 6 und 5, 7, 6, 4, 5, 1, 3, 2, 8, 9, 5 zwischen 4 und 8, 9, 8, 5, 4, 9, 8, 4 zwischen 5 und 2, 3, 2, 4, 5, 3, 2, 5 zwischen 4 und 1, 2, 3, 9, 8, 1, 5, 4, 2, 3, 9, 8, 1, 5 zwischen 1 und 4, 7, 6, 1.

Lösung vom 16.12.
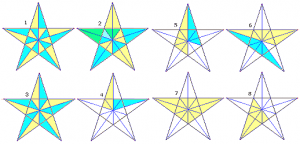
Für die einzelnen Varianten von Dreiecken ergibt sich:
Abbildung 1: Es gibt 20 aneinanderstoßende Dreiecke, an den Spitzen 10 und im Inneren des Fünfecks weitere 10
Abbildung 2: Je 1 Paar anstoßender Dreiecke von 1. gibt ein neues Dreiecke, insgesamt 10
Abbildung 3: 10 aneinanderstoßende Dreiecke
Abbildung 4: Insgesamt 10 Dreiecke, die sich teilweise überlappen
Abbildung 5: Von jeder eingezeichneten Art existieren genau 10 Dreiecke
Abbildung 6: Von der gelb eingezeichneten Dreiecksart gibt es 10, von der anderen 5
Abbildung 7: 5 Dreiecke
Abbildung 8: 10 derartige Dreiecke
In der Summe existieren somit in der Ausgangsfigur genau 100 verschiedene Dreiecke.

Lösung vom 17.12.
Für das Löchersetzen und -füllen muss man x-mal auf die Lochkarte klicken. Die endgültige Lösung ist
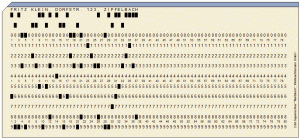Auf den Lochkarten wurden die Ziffern 0 bis 9 durch ein Loch an der Stelle 0 bis 9 markiert. Für die Buchstaben galt, je nach Rechnersystem:
A … I : Loch bei A und 1 bis 9
J … R : Loch bei B und 1 bis 9
S … Z : Loch bei 0 und 2 bis 9
Dabei ist die Zeile A die oberste, die Zeile B die zweite. Für die Sonderzeichen gab es spezielle Codes.

Lösung vom 18.12.
Abgebildet ist eine Halbadder-Schaltung bei der das Signal der oberen Lampe zusätzlich negiert wurde. Damit ergibt sich als Lösung von oben nach unten
0 0 , 1 1 , 1 1, 1 0
In der Realität wird bei einem Halbadder der obere Ausgang natürlich nicht negiert, es sollte aber ein kleines bisschen schwieriger werden.

Lösung vom 19.12.
Die einzelnen Zahlen ergeben sich zwingend logisch.
In der ersten Aufgabe ist das Ergebnis natürlich 0. Bei der Addition von 2 zweistelligen Zahlen kann der evtl. entstehende Hunderter nur 1 sein. Dann folgt in der 7.Zeile, dass der Zehner des Ergebnisses eine 2 sein muss, usw. 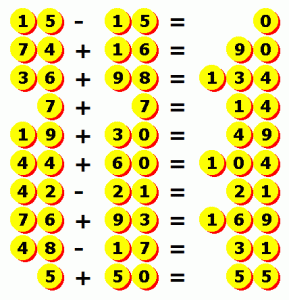usw. Insgesamt erhält man die Lösungen der Gleichungen

Lösung vom 20.12.
Die Hausnummern sind von oben nach unten in Arabisch, Hindi, Tamil, Farsi/Arabisch und Maya geschrieben.
Zusätzlich mit den Erklärungen sind die gesuchten Zahlen damit: 127, 42, 276, 80 und 137.

Lösung vom 21.12.
Dieses Kryptogramm kann man schrittweise lösen.
In der Darstellung (bei Euch können andere Symbole erscheinen, da sie permutieren) können Mond und Herz keine 1 sein, da dann in der 1.Zeile das Produkt auf eines der beiden Symbole enden würde.
Der Mond kann auch nicht 2 oder 3 sein, da die Summe der 2.Spalte dann nicht möglich ist. Nehmen wir an Mond = 4.
Dann ist das Kreuz (Division 2.Zeile) 1 oder 6. 1 ist nicht möglich (Division 3.Spalte), d.h. Kreuz = 6.
In der 2.Spalte wird Herz = 2 und Dreieck = 8. In der untersten Zeile wird für den Kreis = 7. Zuletzt ergibt sich Gesicht = 1 und Pfeil = 3.
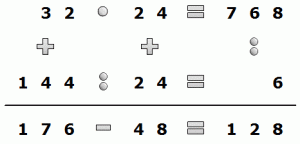Damit ist eine Lösung gefunden. Alle anderen Ansätze Mond > 4 führen zu Widersprüchen.

Begnügt man sich mit den ersten beiden waagerechten Aufgaben
(10*a+b)*(10*b+c)-100*d-10*e-f=0
(100*g+10*c+c)-e*(10*b+c)=0
so ergibt Brute Force mit der möglichen Lösungsmenge {0; 1; …; 9} schon die gesuchte Lösung. Die anderen Gleichungen sind nicht notwendig.

Lösung vom 22.12.
Das Bild ist ein Stereogramm.
Die Lösung „sieht“ man, wenn man versucht durch das Bild hindurch zu sehen, d.h. man blickt in die Ferne. Den Trick mit dem Schielen oder Überkreuzen der Augen kann ich nicht. Ergebnis: ein Dreirad

Lösung vom 23.12.
Das nichtlineare Gleichungssystem
A – B = C ; A + B = D ; B · E = F ; G – H = I / B
kann man schrittweise lösen.
Aus der 1.Gleichung folgt A > 2, aus der 2. A < 8
Aus der 3.Gleichung folgt, dass weder B noch E = 1 sein können; aus der 4.Gleichung ergibt sich, dass B nur noch 2, 3 oder 4 sein kann; andernfalls müsste I zweistellig sein, was nicht geht.
Fall a) B = 4 erzwingt I = 8. Dann müsste aber E 1 oder 2 sein. Beides führt zum Widerspruch da dann F = B ist oder F = 8.
Fall b) B = 2 ergibt A – 2 = C ; A + 2 = D ; 2E = F ; 2G – 2H = I
Mit E = 3 wird F = 6. Mit A = 4 –> C = 2, A = 5 –> C = 3 ergeben sich Widersprüche. A müsste 7 sein, d.h. C = 5 , D = 9. Damit verblieben für G, H, I nur noch die Wert 1, 4 und 8. Keine mögliche Belegung erfüllt 2G – 2H = I, d.h. B kann nicht 2 sein.
Damit verbleibt nur der
Fall c) B = 3
A – 3 = C ; A + 3 = D ; 3E = F ; G – H = I / 3
Wäre F = 9 dann E = 3 (Widerspruch), d.h. F = 6, E = 2, I = 9.
A – 3 = C ; A + 3 = D; G – H = 3
Für A verbleibt nur noch 4 mit C = 1 und D = 7. G ist dann 8 und H = 5.
Insgesamt lautet der Code also 431726859.

Adventskalender 2014

Lösung 1.12.: 
Folgende Geschenke müssten verschoben werden:
Eva nach rechts, Melanie oben nach links, Kerstin rechts nach links neben Eva, Susi oben nach rechts und links zwischen die 2 Kerstin, Susi oben nach links, Anja nach rechts zur zweiten Anja, Iren zur 2.Iren, Susi zur Susi und Kerstin bzw. Eva zusammenschieben.

Lösung 2.12.: 
Es gibt mehrere Möglichkeiten. Eine davon ist

Lösung 3.12.:
Die 20 blauen Kugeln links oben müssen durch das Gitter fallen und sich in Diamanten verwandeln. Dazu muss man sich einen Weg vorbei an den 2 Monstern suchen. Ansonsten muss man eben „vorsichtig“ zum Ausgang laufen.

Lösung 4.12.:
E kann nicht 2 oder größer sein, da selbst mit Übertrag die 2 fünfstelligen Zahlen THREE kein sechsstelliges ELEVEN ergeben. Man kann durch analoge Überlegung erkennen, dass T mindestens 4 sein muss. T=9 ist nicht möglich, da H+H eine Zahl mit Einerziffer 1 ergeben soll, d.h. ein Übertrag auftritt.
Damit sind die Möglichkeiten schon eingeschränkt. Mit Brute Force erhält man, je nach Berücksichtigung der Einschränkungen, verschiedene Lösungen.
Mein (wirklich nicht elegantes) Delphi-Programm im Anhang liefert nach Start sofort die eindeutige Lösung:
THREE TWO ONE ELEVEN
84611 803 391 171219
Selbst ohne Test auf die Zehnerstelle von ELEVEN = 1L1V1N erhält man 19 Lösungen, von denen nur die letzte Zeile korrekt ist.
D.h.: T=8, H=4, R=6, E=1, W=0, O=3, N=9, L=7 und V=2

Lösung 6.12.: 
Abfolge:  Schalter „senkrecht“, danach „hinten“, 3x „rechts“, „waagerecht“, 3x „oben“, einmal „mitte“ (in der Mitte der 3 Schalter) und abschließend 3x „vorn“.

Lösung 7.12.:
Mögliche andere Lösungen entstehen durch Drehung und Spiegelung.

Lösung 8.12.:
In der achten Zeile steht  … 69519515116094…
Die hervorgehobene 5 ist falsch und müsste eine 4 sein. Damit ist die 392.Stelle falsch.

Lösung 9.12.:
Eine mögliche Lösung wäre:

222333000333000100030001123 31112211100333312210301330332 2212223222111000000222222333 0001220000030001121122322222 2330322123301003330012321110 1200000300011211223222222330 32123331100333000001222232111 0100003000112112232222223330 0120000030001121122322222233 0321233100330000013221023222 1110000331122223333000001222 2321133000011112222211000000 1003303322212332322211012000 0030001121122322222233032212 303210003330000012222321110 010003000112112232222223330 012000003000112112232222223 303221230003300000132222211 121100000010033033222321012 222200003000011211223222222 330321230000100030003321012 2212330322223211300001112223 222200001000300001123032221 2330322200011001111223010333 03222123303201100111221110033 3330322232332212321133000001 111222232220033300001220001 11233032111222221122211103323 00000000001033303222333222 1232113300000111122223220333 0000122000111233032011001112 222222212322110323000000000 0103330322232101222222201100 1110332300000103330322232101 222222000003333221232113300 0011112223201000333222321133 0000111000111222221103230000 103330322232101222220000300 01111112332301033303222321012 222

mit 0 = hoch, 1 = rechts, 2 = runter, 3 = links.

Lösung 12.12.:
Die Aufgabe entstammt dem Wasan, der „japanischen Mathematik“ während der Edo-Zeit (1603-1867). Eine besondere Form des Wasan ist das Sangaku, d.h. Holztafeln, auf denen geometrische Rätsel beschrieben wurden. Diese Tafeln wurden in Tempeln als Dank für eine Shinto-Gottheit ausgehängt.

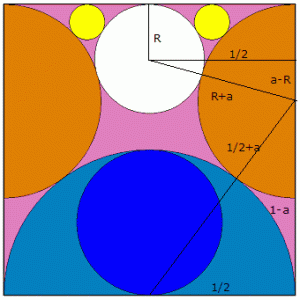Zeichnet man in die Darstellung einige Strecken ein, u.a. die Verbindungslinien der Kreismittelpunkte und Senkrechte, so entstehen zwei rechtwinklige Dreiecke. Das untere Dreieck in der Abbildung ermöglicht den Radius der roten Halbkreise zu berechnen.
Sind die Quadratseite = 1 und der rote Kreisradius = a, so wird mit dem Satz des Pythagoras
(12+a)²=(12)²+(1−a)²
Mittels binomischer Formeln; das Quadrat a² hebt sich heraus; wird a = 1/3.
Das 2.Dreieck ist schwieriger zu finden. Ist R der gesuchte Kreisradius, so wird für die Hypotenuse R+a = R+1/3 und für die Katheten 1/2 sowie 1/3-R, d.h.
(R+13)²=(12)²+(13-R)²
Diese lineare(!) Gleichung hat nur eine Lösung: R = 3/16.

Lösung 13.12.:
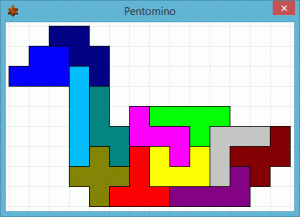
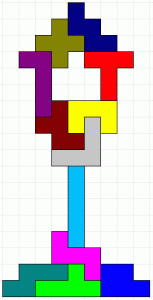
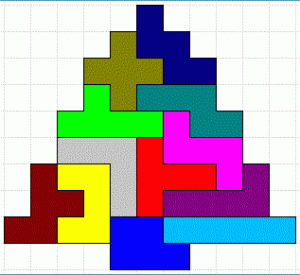Der Weihnachtsbaum sollte aus Pentomino-Bausteinen zusammengesetzt werden. Insgesamt gibt es 532 verschiedene Möglichkeiten die Teile entsprechend anzuordnen. Eine Lösung ist in der Abbildung zu sehen.

Lösung 15.12.:
Der kodierte Text ist MTNYAEYISABGI.
Betrachtet man die Verschlüsselungsscheibe, so tritt im äußeren Ring kein Y auf, d.h. innen muss der Geheimtext eingestellt werden, außen der Klartext abgelesen werden. Da es den Zurücksetzen-Schalter gibt, muss die angezeigte Lage der Scheiben wichtig sein. Das ist sie auch, denn es ist die Starteinstellung.
Damit erhält man für das M innen als ersten Klartextbuchstaben das C außen. Die Innenscheibe dreht man um 1 gegen die Uhrzeigerrichtung  . Und damit erhält man als Lösung

COGITOERGOSVM

Da im klassischen Latein U=V ist, wird also (hier mit Leerzeichen, die nicht eingegeben werden sollten):

COGITO ERGO SUM

d.h. das berühmte Zitat (Ich denke also bin ich ; Je pense donc je suis) vom französischen Mathematiker und Philosophen René Descartes. COGITOERGOSVM ist aber auch richtig.

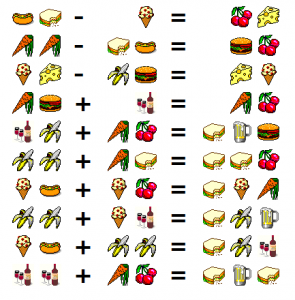Lösung 17.12.:
Lösung bezieht sich auf die links abgebildete Aufgabe.
Bei der Addition von 2 zweistelligen Zahlen muss ein dreistelliges Ergebnis mit einer 1 beginnen, d.h. das Sandwich ist eine 1.

Nur das Bierglas und der Hamburger treten nicht als erste Ziffer eines Summanden auf. Aber nur das Bierglas ist ausschließlich in den Ergebnissen zu finden. Es muss die 0 sein, andernfalls würde es sich „verraten“; dass es die Einerstelle als Summand oder Subtrahend nicht verändert.
Damit ergeben sich u.a. die zwei Aufgaben

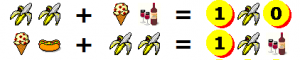
In der ersten Zeile wird der erste Summand mit einem Zehner=Banane mit einer anderen zweistelligen Zahl (Zehner=Eistüte) so addiert, dass auch im Ergebnis wieder eine Banane als Zehner auftritt. Dies ist nur möglich, wenn die Eistüte die 9 ist.
Danach verändern sich alle anderen Aufgaben so, dass durch relativ einfache Addition und Subtraktion die restlichen Ziffern gefunden werden können. Vom oben nach unten ergibt sich:
81 – 9 = 72 ; 55 – 18 = 37 ; 92 – 63 = 29 ; 53 + 4 = 57 ; 46 + 57 = 103 ; 66 + 51 = 117 ; 98 + 97 = 195 ; 66 + 94 = 160 ; 98 + 66 = 164 ; 44 + 57 = 101

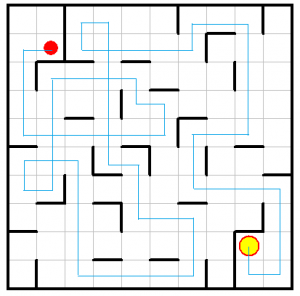
Lösung 19.12:
Das Kugelrollspiel löst man von „hinten“, d.h. man beginnt beim Ziel und prüft von welchem Ort aus die Kugel sich bewegen könnte. Dann erhält man die Zugfolge mit lurululdldrdrurulurdldr ; d = down, r = right, u = up und l = left
oder als Bild (siehe links).

Lösung 20.12.:
Das gesuchte Geschenk vom 20.12. zu ermitteln, erforderte einen QR-Code-Reader.
Dann erhält man die Lösungsbuchstaben

ABDEEEHILLMNNOS

Nun muss man die Buchstaben noch durcheinander würfeln. Gesucht war …

MODELLEISENBAHN

und das ist wirklich ein schönes Geschenk.

Lösung 21.12.:
Das Märchen, dessen Text am 21.12. vollkommen durcheinander gekommen war, ist „König Drosselbart“.
1) algorithmische Lösung; d.h. der Text wird entschlüsselt
Hier war die Gartenzaunkodierung das Kodierungsverfahren, wie bei der Ankündigung des AGS 2014.
Allerdings gibt es zwei Änderungen.
Erstens ist die Codezahl 5, d.h. es werden 5 Zeilen berücksichtigt, und zweitens wurden dieses Mal alle Zeichen, d.h. auch die Leer- und Sonderzeichen, „verwurschtelt“. Dass alle Zeichen verändert werden, erkennt man auch daran, dass sehr viele Einzelbuchstaben im Codetext auftreten, d.h. die Satzstrukturen nicht mehr vorhanden sind.

2) visuell-kognitiv; Hinsehen, Überlegen und Märchenkennen
Da man ohne die Idee des Kodierungsverfahrens keine Lösung erzielt, gab es noch ein Hintertürchen, die Abbildung. Auf der Abbildung sind eine Prinzessin und drei Herren, Edelmänner natürlich, zu sehen; einer dick wie ein Weinfass, einer zu lang („lang und schwank hat keinen Gang“) und einer ziemlich kurz („kurz und dick hat kein Geschick“). Kennt man sich in Grimms Märchen aus, wird klar, dass es „König Drosselbart“ ist.
Die Abbildung stammt von einem Märchen-Briefmarkensatz. Mit einer Google-Suche findet man das Bild relativ schnell.

Lösung 23.12.:
Die Lösung ist einfach, wenn man Fan von „The hitchiker’s guide to the galaxy“ („Per Anhalter durch die Galaxie“) von Douglas Adams ist.

Im Text steht, dass der Doctor murmelt: „DNA, 42, DNA, 42, …“
Die 42 ist in diesem Werk „… the ultimative answer to life, the universe, and everything, …“ („ultimativ letzte Antwort zum Leben, zum Weltall und allen anderen Dingen“). Das ist der wichtigste Hinweis auf das Buch. DNA sind aber die drei Anfangsbuchstaben von Douglas Noël Adams. Und Noël = Weihnachten passt ja hervorragend.
Welches Datum ist nun gesucht?

Die merkwürdigen Schriftzeichen sind die Zahldarstellung von 11031952 in der Kunstsprache Gallifrey, der Sprache des Heimatplaneten des Doctors in der Kultserie „Doctor Who“.
Wenn man gar keine Idee hatte, konnte man zumindest 11xx1xxx erraten, denn bei 8 Zeichen wird die Jahresangabe wohl mit einer 1 losgehen. Damit sind auch die ersten 2 Zeichen eine „1“.
Das Ergebnis ist der Geburtstag von Douglas Noël Adams, d.h. der 11.März 1952. Einzugeben war damit 11031952.

Adventskalender 2015

Lösung 1.12.:
Melanie (oben) nach links, Maria (rechts) 1 nach links, Kerstin (links) zwischen Eva und Maria,
Maria (links) nach rechts, Kerstin (rechts) 1 nach links, Kerstin (links) 1 nach rechts, Eva (links) 1 nach rechts,
Anja (links) links neben Eva, Sophia (links) nach rechts über Kerstin, Sophia (rechts) 2 nach links,
Kerstin (rechts) nach links, Eva (oben) nach links, Anja (rechts) nach links

Lösung 3.12.;
Die Lösung ist OSTERHASE um 18:30.
Das Gerät, mit dem die Nachricht übertragen wurde, soll ein Chappe-Telegraf sein.
Diese optische Telegrafie-Vorrichtung benutzte zur Zeichenübermittlung schwenkbare Signalarme. An einem fünf Meter hohen Mast mit zwei Querbalken war jeweils ein weiterer schwenkbarer Balken am Ende der Querbalken angebracht, der je nach Position unterschiedliche Buchstaben signalisierte.
Die erste erste reguläre Telegrafenlinie zwischen Paris und Lille wurde 1794 eingerichtet, 22 Stationen auf 270 km. Die Laufzeit für die Übertragung eines einzelnen Buchstabens lag bei nur zwei Minuten.
Im Netz findet man u.a. diese Kodiertabelle (allerdings auch abweichende Darstellungen).

Lösung 5.12.:
Die Lösung ist UN=81 ; HUIT=2864 ; ONZE=3107.
Aus UN + UN + UN + HUIT = ONZE
folgt sofort, dass U mindestens 7, wahrscheinlich eher 8, sein muss. (7 nur, wenn I mindestens 8 ist)
Andernfalls gibt es bei der Addition keinen Übertrag, d.h. eine Erhöhung des Tausenders von HUIT. N kann nicht 0 sein, da sich der Einer ändert.
O kann nicht 9 sein, da sonst die 2.Gleichung keine Lösung mehr hat, d.h. O = 2,…,8 und H = 1,…,7.
Fallunterscheidung:
H = 1 und U = 8 ergibt 8N + 8N + 8N + 18IT = 2NZE , Widerspruch da dann N = 0 oder 1
H = 1 und U = 9 ergibt 9N + 9N + 9N + 19IT = 2NZE , Widerspruch da dann N = 1 oder 2
H = 2 und U = 8 führt zu 8N + 8N + 8N + 28IT = 3NZE.
Probieren mit N = 1 wird 81 + 81 + 81 + 28IT = 31ZE und Z + E = 7. Die Möglichkeiten für E, Z mit 7;0, 3;4 oder 4;3 führen zur Lösung.

Lösung 6.12.:
Eine mögliche Kombination der Schalter ist: 1x senkrecht, 1x hinten, 3x rechts, 3x unten mitte, 2x unten, waagerecht, 3x oben , 1x mitte mitte, 1x vorn

Lösung 8.12.:
Es war das Josephus-Problem. Bei 36 Personen ergibt sich dort die optimale Abzählweite von 13.
Das kann man auch mit Papier und Stift wieder ermitteln. Einfach aufmalen und dann mit einer Abzählweite 2, 3, 4, … testen.
Es hilft auch eine kleine Routine:
procedure TForm1.Button1Click(Sender: TObject);
var i,j,r,personen:integer;
   gefunden:boolean;
begin
   personen:=strtoint(edit1.Text);
   i:=2;
   gefunden:=false;
   repeat
      r:=0;
      for j:=1 to personen do r:=(r + i) mod j;
      if r=0 then gefunden:=true;
      inc(i);
   until gefunden or (i>=personen);
   if gefunden then label1.Caption:=inttostr(i-1)
      else label1.Caption:='kein Optimum';
end;

Lösung 9.12.:
Dieses Jahr waren es nur wenige Kisten, die bewegt werden mussten, so dass es nicht ganz so stupide wurde.
Eine mögliche Zugfolge ist: 0=hoch, 1=rechts, 2=runter, 3=links
22223303322212300121002330011101212223330332210301210023300112221110003032
33322222330121030121032333001013232211110100033222012100223332210301210301
2102111000330030012220011003032223210122003303001012222321012010110333032
223210110111223010330333221101033032222003300333211011122330301101222011223
303203033332210301110111223303011012222

Lösung 11.12.:
Die Kodierung erfolgt über die klassische Jefferson-Walze.
Zum Entschlüsseln musste die Nachricht TTYQVNCALYNYNMXZWU Buchstabe für Buchstabe an den einzelnen Scheiben eingestellt werden. Das geht, in dem man unter oder über einer der Scheiben mit der Maus klickt. Dann „rollt“ die Scheibe einen Buchstaben weiter.
Sind alle Buchstaben des „Geheimtextes“ eingestellt, befindet sich irgendwo auf der Walze der Klartext.
Um diesen zu sehen, klickt man wiederholt auf Walze vorwärts oder rückwärts.
Die Nachricht ist: ESGIBTKEINENSCHATZ
Das ist „überraschend“, wo doch jeder weiß, dass John Flint auf Stevensons „Schatzinsel“ einen Riesenschatz versteckt hat.

Lösung 12.12.:
Die Gesamtfläche der gelben Möndchen ist die Fläche von 8 Halbkreisen, reduziert um die 8 weißen Kreissegmente.
Die Kreissegmente ergeben sich als Differenz des Umkreisflächeninhalts und des Achteckflächeninhalts.
Entweder löst man alles Schritt für Schritt oder man greift zur Formelsammlung. Ist r = 4 der Umkreisradius wird:
Kreisfläche = π r²
Achteckfläche = √2 r²
Seite des Achtecks a = r/√(2-√2)
8 Halbkreisflächen = π r² (2-√2)
8 Möndchen = π r² (2-√2) − π r² + √2 r²
Einsetzen ergibt mit r = 4 als gesuchte Fläche 24,4341…

Lösung 13.12.:

Lösung 15.12.:
Der kodierte Text ist TNQX2VLQTZON.
Da im inneren Ring keine 2 auftritt, muss der Geheimtext außen eingestellt werden und der Klartext innen abgelesen werden. Da es den Zurücksetzen-Schalter gibt, ist die angezeigte Lage der Scheiben wichtig, d.h. sie ist die Starteinstellung. Damit erhält man für das T außen als ersten Klartextbuchstaben das E innen.
Vor zwei Jahren musste man die äußere Scheibe für den jeweils nächsten Buchstaben um ein Feld in Uhrzeigerrichtung drehen, im Vorjahr entgegen der Uhrzeigerrichtung.
Im Text steht: „Dieses Jahr kann er aber sich nicht so richtig entscheiden.“
Folglich wird einmal in Uhrzeigerrichtung um 1 Feld gedreht und dann wieder entgegen, usw. usf. oder entsprechend entgegengesetzt. Von den 2 Möglichkeiten führt eine zu: EXORIENTELVX
Da im klassischen Latein U=V ist, kann auch EXORIENTELUX („Aus dem Osten kommt das Licht“) eingegeben werden.

Lösung 17.12.:
Bei der Zahlenaufgabe ist das erste Symbol der dreistelligen Zahl logischer Weise die 1. Da dort eine einstellige mit einer zweistelligen Zahl addiert wird, kann das Ergebnis nicht größer als 109 sein, d.h. das dreistellige Ergebnis muss (2 gleich Ziffern) die 100 sein.
Daraus ergibt sich auch, dass die zweistellige Zahl mit 9 anfängt.
Im Ergebnis gibt es nun eine Aufgabe: a + bc = 91. Dort muss b = 8 sein. Die restlichen Ziffern folgen dann durch einfache Additionen.

Lösung 19.12.:
Mit der Bezeichnung l=left, d=down, r=right, u=up ist die kürzeste Zugfolge: ldruludlurdrulululdrurdldrdlu
oder als Bild

Lösung 20.12.:
Da er nur waagerecht nach rechts, senkrecht nach oben und diagonal von links unten nach rechts oben laufen kann, liegt hier ein gerichteter Graph von W nach A vor. Für ein einzelnes Quadrat ABCD mit Diagonale gilt dann:

Ist a die Anzahl der Möglichkeiten nach A zu gelangen, b die nach B und c die nach C, so gibt es genau d = a+b+c Möglichkeiten nach D zu gelangen.

Es ist offensichtlich, dass man von B und C nur auf einem Weg nach D kommt, damit ist die Gesamtzahl b+c. Von A kann man auch nur auf eine Art nach D gelangen, nämlich diagonal. Die Wege A->B->D und A->C->D sind nicht mehr zu berücksichtigen, da diese schon bei den Möglichkeiten b und c eingerechnet sind. D.h., insgesamt d = a+b+c.
Beginnt man nun links unten im Graphen und berechnet für die rechte obere Ecke jedes Quadrates die Summe der dahinführenden Wege (3, bzw. wenn der Eisbär stört 2), so erhält man

Willy kann also auf 152 verschiedenen Wegen zum Weihnachtsmann gelangen, ohne gefressen zu werden.
Die Gesamtzahl der Wege wird durch die Delannoy-Zahlen bestimmt. Die Delannoy-Zahlen werden definiert durch:

D(a,b)=D(a−1,b)+D(a,b−1)+D(a−1,b−1)

wobei D(0,0) = 1 ist. Das ist die von mir oben gegebene Erklärung für das Lösen per Hand.
Diese Zahlen geben die Anzahl der möglichen Wege vom Punkt (0,0) zum Punkt (a,b) an, wenn ausschließlich Schritte (1,0), (0,1) und (1,1) möglich sind.
Für die ersten Delannoy-Zahlen D(n,n) ergibt sich für n = 0,1,2,3,…
1, 3, 13, 63, 321, 1683, 8989, 48639, 265729, 1462563, 8097453, 45046719, 251595969, 1409933619, 7923848253, 44642381823, 252055236609, 1425834724419, 8079317057869, 45849429914943, 260543813797441, …

Lösung 23.12.:
Analyse des Rätsels:
1) Damezug oder Königszug
a) Ein Damezug zu a2 bis e2 oder ein Königszug erzwingt Th2 und kein Matt in nur noch 4 Zügen.
b) Ein Damezug f2 bis h2 führt zum Dameverlust.
c) Dd3 Kh2 ergibt kein Matt in nur noch 4 Zügen
d) Dg6+ Kf2 führt zu Matt in nun 5, d.h. insgesamt 6 Zügen

2) Bauernzug
a) Bf4 Th2 Dxh2 … führt zu Remis
b) Bf4 Th2 Dd3 Kg2 … ergibt kein Matt in noch 4 Zügen
c) Bf4 Th2 Dg6 Kf2 … ergibt kein Matt in noch 4 Zügen

3) Springerzug
Sh3 Kxh3 führt mit Kd4 … zu Matt in nun noch 5 Zügen
Die einzige noch verbleibende Lösung ist:
Se2+ Kxf3 Sf4 Ke3 De2++
Se2+ Kxf3 Sf4 Kg3 Dg2++
Se2+ Kxf3 Sf4 Kg4 Dg6+ Kf3 Dg2+ Ke3 De2++ , wenn der Nikolaus „gut“ spielt.
Also ist Se2 die richtige Lösung.

Adventskalender 2016

Lösung 1.12.:
Sophia (links) nach rechts, Susi (oben, 6.Reihe) links, Melanie (6.Reihe) links, Sophia (7.Reihe) ganz nach links, Melanie (3.Reihe) 3x rechts, Anja (3.reihe) 2x rechts, Susi (7.Reihe) links, Anja links, Sophia (5.Reihe) rechts, Sophia (4.Reihe) rechts, Sophia (8.Reihe) 2x links

Lösung 3.12.:
A nach C, C nach B, A nach C, C nach B, B nach A, C nach B, A nach C, C nach B, A nach C, C nach B
Es gibt weitere Möglichkeiten, aber mit 10 Zügen ist es das kürzeste Mögliche.

Lösung 5.12.:
HOCUS + POCUS = PRESTO
Ist die Summe zweier 4stelliger Zahlen 5stellig, so ist die 1.Ziffer von PRESTO eine 1, folglich H eine 9, d.h.
9OCUS + 1OCUS = 1RESTO , d.h.
OCUS + OCUS = RESTO
R muss Null sein, da bei einem Übertrag maximal 1 entstehen kann. 1 ist aber schon vergeben.
OCUS + OCUS = ESTO
O muss gerade sein (2*S), d.h. 2, 4, 6 oder 8. 6 und 8 entfallen, da sonst durch den Übertrag R = 1 wäre. Damit gibt es zwei Möglichkeiten
1) 2CUS + 2CUS = EST2 (*)
2) 4CUS + 4CUS = EST4
Im 1.Fall muss S = 6 sein, S = 1 entfällt. Im 2.Fall kann S = 2 oder 7 sein.

Dafür gibt es wieder zwei Fälle
2A) 4CU2 + 4CU2 = E2T4 ; entfällt, da C dann 1 oder 6 sein müsste
2B) 4CU7 + 4CU7 = E7T4 ;
4CU7 + 2CU7 = E7T4 ; d.h. E = 6
4CU7 + 2CU7 = 67T4 ; und somit C = 3 und U >= 5
43U7 + 23U7 = 67T4 ; U = 6, 7 geht nicht , also U = 8, dann wird T = 6 Widerspruch

Folglich gilt der 1.Fall (*)
2CU6 + 2CU6 = E6T2
U kann noch sein 3, 4, 5, 7, 8 ; durch den Übertrag entfallen 4 und 5 und da kein neuer Übertrag entstehen darf, entfallen auch 7 und 8
2C36 + 2C36 = E672
Damit müssen C = 8 und E = 5 sein.
HOCUS = 92836
POCUS = 12836
PRESTO = 105672

Lösung 8.12.:
Lösung = 2168
Klar ist, dass das gesuchte Jahr, wie 2016, an einem Freitag beginnen muss. Ebenso logisch ist, dass es ein Schaltjahr sein muss. Allein mit diesen Regeln ergibt sich 2044. Allerdings widerspricht der Osterhase!
Warum wohl? Ganz einfach, auch Ostern soll am gleichen Tag liegen.
Damit reduziert sich die Aufgabe auf die Suche nach einem Schaltjahr, bei dem am 27.März Ostersonntag ist.
Entweder man nutzt einen der vielen Osterrechner im Netz, oder mein Programm 😉 oder man schreibt schnell ein kleines Programm.

Lösung 11.12.:

Lösung 12.12.:
von A bis E: Gift, Schokolade, Schokolade, Gift, Schokolade.

Lösung 13.12.:
mögliche Zugfolge der Scheiben: A-C, A-D, A-B, D-B, C-B, A-D, A-C, D-C, A-D, C-A, C-D, A-D, B-A, B-C, B-D, C-D, A-D

Lösung 16.12.:
Die äußere Scheibe ist je Buchstabe um 1 in Uhrzeigerrichtung zu drehen. Dann ergibt sich:
FROHEWEIHNACHTEN

Lösung 20.12.:
Der Euro-Betrag des korrekten Wechselgeldes sei euro, der Cent-Betrag cent. Das Wechselgeld ist also 100 euro + cent. Das vertauschte Wechselgeld ist demnach euro + 100 cent, alles in Cent gerechnet.
Damit ergibt sich die Gleichung: euro + 100*cent = 2*(cent + 100*euro) + 5
euro + 100*cent = 2*(cent + 100*euro) + 5
euro + 100*cent = 2*cent + 5 + 100*(2*euro)
Euro- (der Summand mit dem Faktor 100) und Cent-Betrag müssen auf beiden Seiten der Gleichung identisch sein, wodurch sich zwei Gleichungen ergeben:
euro = 2*cent + 5
cent = 2*euro
Einsetzen ergibt euro = 4*euro + 5 , d.h. euro = -5/3.
Das ist aber ein Widerspruch, da der Euro-Betrag ganzzahlig und größer Null sein muss.
Wo ist der Denkfehler?
Es ist der Übertrag von 2*cent+5, der auftritt wenn cent > 47 ist. In diesem Fall verändern sich die 2 Gleichungen zu
euro = 2*cent + 5 – 100 ; Übertrag 100 Cent subtrahieren
cent = 2*euro + 1 ; Übertrag 1 € addieren
d.h. euro = 2*cent – 95
cent = 2*euro + 1
mit der Lösung
euro = 2*(2*euro +1)-95 , d.h. euro = 31.
cent = 63 folgt automatisch.

Lösung 22.12.:
Die Aufgabe verwendete eine einfache Form der visuellen Kryptografie.
D.h., die beiden Bilder müssen absolut genau und transparent übereinander gelegt werden. Damit ergibt sich
also: Weihnachten 2016