Das Braess-Paradoxon der Spieltheorie veranschaulicht, dass eine zusätzliche Handlungsoption bei rationale Entscheidung zu einer Verschlechterung der Situation für alle führen kann. 1968 veröffentlichte der deutsche Mathematiker Dietrich Braess dieses Paradoxon.
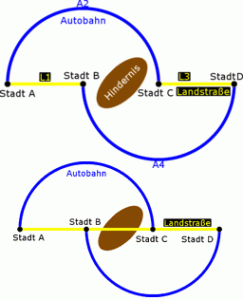Gegeben sei ein Straßennetz, dass vier Städte A, B, C und D miteinander verbindet.
Von A nach C und von B nach D verläuft jeweils eine relativ lange Autobahn, auf der die Fahrtzeit kaum von der Verkehrsdichte abhängt.
Bei einer Verkehrsdichte (in Tausend Autos pro Stunde) beträgt die Fahrtzeit je Fahrer
- tAC(x) = tBD(x) = 50 + x Minuten
Die Städte A und B sind wie die Städte C und D durch eine Landstraße verbunden, mit einer Fahrtzeit je Fahrer
- tAB(x) = tCD(x) = 0 + 10 x Minuten
Alle Autofahrer wollen von A nach D fahren, wobei jeder Fahrer den für sich schnellsten Weg wählt. Es stellt sich ein Nash-Gleichgewicht ein, bei dem die Hälfte der Fahrer die Strecke über Stadt B, die andere Hälfte über Stadt C fährt. Bei 6000 Autofahrern fahren somit auf jeder Strecke 3000 Autos. Die Fahrtzeit beträgt für jeden 83 Minuten.
Wird zusätzlich eine Straße zwischen den Städten B und C gebaut mit der Fahrzeit
- tBC(x) = 10 + x Minuten
so fahren auch Autos direkt von B nach C. Das nun entstehende Gleichgewicht ergibt
- 2000 Fahrer wählen die Strecke ABD
- 2000 Fahrer wählen die Strecke ACD
- 2000 Fahrer wählen die Strecke ABCD
Durch die vielen Fahrzeuge auf den Landstraßen erhöht sich die Fahrtdauer für alle Fahrer auf 92 Minuten, d.h. länger als ohne die Neubaustrecke.
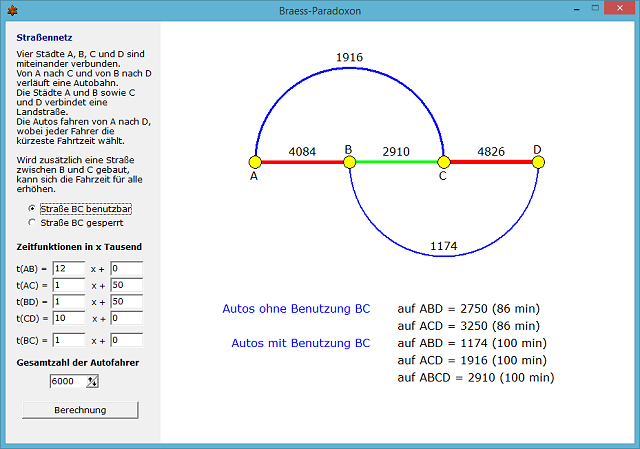
In diesem Teilprogramm wird dieses Paradoxon demonstriert.
Für die fünf Teilstrecken können Sie die Koeffizienten linearer Zeitfunktionen eingeben. Dabei entspricht x eintausend Autofahrern je Stunde. Für die Berechnung des Nash-Gleichgewichts muss außerdem die Gesamtzahl der Autofahrer festgelegt werden.
Mit dem Schalter Berechnung ermittelt das Programm die zu erwartenden Fahrerströme je Strecke, zum einen ohne Zusatzstrecke BC, zum anderen mit dieser.
Interessant ist, dass bei mittlerem Verkehrsaufkommen die neue Strecke sehr oft zu einer Erhöhung der Fahrtzeit für alle führt; eine paradoxe Situation.
| Braess-Paradoxon |
|---|
 |
| Herunterladen |
Download
Dieser Programmteil von „Mathematik alpha“ existiert auch als einzelnes Programm.