 Im französischen Fernsehen ist eine Spielshow besonderer Art sehr beliebt: Aus einer Menge vorgegebener ganzer Zahlen ist durch schrittweise Addition, Subtraktion, Multiplikation oder Division eine Zielzahl zu ermitteln. Dabei darf und muss jede gegebene Zahl und jedes Zwischenergebnis genau einmal verwendet werden!
Im französischen Fernsehen ist eine Spielshow besonderer Art sehr beliebt: Aus einer Menge vorgegebener ganzer Zahlen ist durch schrittweise Addition, Subtraktion, Multiplikation oder Division eine Zielzahl zu ermitteln. Dabei darf und muss jede gegebene Zahl und jedes Zwischenergebnis genau einmal verwendet werden!
Beispiel: Aus den Zahlen 1 bis 6 ist die 278 zu konstruieren.
4 · 5 = 20 ; 3 + 20 = 23 ; 23 · 6 = 138 ; 1 + 138 = 139 ; 139 · 2 = 278
Als einzelne Gleichung würde sich damit ((3 + 4 · 5) · 6 + 1) · 2 = 278 ergeben.
Wie schwierig die Aufgabe ist, erkennt man vielleicht daran, dass zum einen die Lösung nicht immer eindeutig ist, mitunter aber auch keine existiert, und zum anderen allein für sechs Ausgangszahlen rund 21 Millionen Möglichkeiten der Kombination von Zahlen und Operationen existieren.
Liegen sogar acht Zahlen vor, wird das Problem um ein Vielfaches schwieriger (444,4 Milliarden Möglichkeiten). Gegenwärtig erscheint es so, dass die Suche nach einer solchen Lösung zu den NP-Problemen der Informatik gehört.
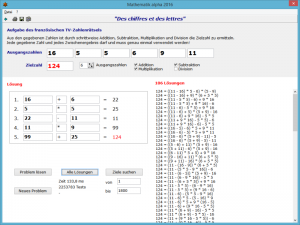
In diesem Programmteil ermittelt das Programm eine, sofern existierende, entsprechende Lösung. An den Pfeilschaltern stellen Sie die Anzahl der Ausgangszahlen ein, die zufällig ermittelt werden, aber auch von Ihnen direkt eingegeben werden können.
Wählen Sie Problem lösen, sucht das Programm nach einer Lösung. Sehr oft werden Sie schnell ein Ergebnis erhalten, jedoch kann es durchaus auch sehr viel Rechenzeit benötigen. Bei acht Ausgangszahlen benötigt der Nachweis, dass keine Lösung existiert, auch auf einem 2,2-GHz-Computer mehrere Minuten Zeit. Die Suche können Sie jederzeit abbrechen.
Hat man die Kandidaten im französischen Fernsehen einmal gesehen, so kann man nur bewundernd staunen, mit welcher Geschwindigkeit dort Lösungen gefunden werden. Es ist äußerst bedauerlich, dass eine derartige Spielshow im deutschen Fernsehen keinen Erfolg haben würde – zum einen, da die meisten deutschen Zuschauer wahrscheinlich das Spielkonzept nicht verstehen würden und zum anderen, weil sie völlig gelangweilt wären, da sie keine Chance hätten, aktiv an der Show teilzunehmen.
Mit dem Prinzip „Des chiffres et des lettres“ sind auch interessante zahlentheoretische Fragen verbunden. Zum Beispiel kann nach der jeweils kleinsten natürlichen Zahl z gesucht werden, die sich nicht durch die Ausgangszahlen 1, 2, 3, …, n auf die genannte Weise konstruieren lässt. Dabei findet man für n = 4, 5, 6, 7 und 8 als kleinste z = 29, 76, 284, 1413 sowie 7187.
Folge berechnen
Solche Folgen von Zerlegungen können Sie auch vom Programm berechnen lassen. Tragen Sie dazu Ausgangszahlen
und unter von … bis einen Suchintervall ein. Klicken Sie nun auf den Schalter Ziele suchen, werden die Ausgangszahlen auf eine kontinuierlich ansteigende Zielzahl angewandt und in der Liste angezeigt.
Die Berechnung stoppt erst, wenn für jede Zahl des Intervalls eine Lösung gefunden wurde oder sich ist, dass es keine weiteren Lösungen gibt bzw. wenn Sie den Vorgang mit dem Abbruch-Schalter unterbrechen.
Alle Lösungen berechnen
Für eine solche Aufgabenstellung kann es auch mehrere Lösungen geben, teilweise sogar sehr viele.
Möchten Sie (theoretisch) alle möglichen Lösungen berechnen lassen, so markieren Sie das Feld alle Lösungen suchen.
Das Programm versucht nun, alle Kombinationen der Operanden und Operationszeichen zu finden und trägt diese in die untere Liste ein.
| Des chiffres et des lettres |
|---|
 |
| Herunterladen |
Download
Dieses Teilprogramm kann als eigenständiges Programm aufgerufen werden.