 Johannes Kepler berichtete 1614, wie er auf seine Betrachtungen zu der nach ihm benannten Fassregel verfiel:
Johannes Kepler berichtete 1614, wie er auf seine Betrachtungen zu der nach ihm benannten Fassregel verfiel:
„Als ich im November des letzten Jahres meine Wiedervermählung feierte, zu einer Zeit, als an den Donauufern bei Linz die aus Niederösterreich herbeigeführten Weinfässer nach einer reichlichen Lese aufgestapelt und zu einem annehmbaren Preis zu kaufen waren, da war es die Pflicht des neuen Gatten und sorgenden Familienvaters, für sein Haus den nötigen Trank zu besorgen.
Als einige Fässer eingekellert waren, kam am vierten Tag der Verkäufer mit einer Messrute, mit der er alle Fässer, ohne Rücksicht auf ihre Form, ohne jede weitere Überlegung oder Rechnung, ihrem Inhalt nach bestimmte.
 Die Visierrute wurde mit ihrer metallenen Spitze durch das Spundloch quer bis zu den Rändern der beiden Böden eingeführt, und als die beiden Längen gleich gefunden worden waren, ergab die Marke am Spundloch die Zahl der Eimer im Fass.
Die Visierrute wurde mit ihrer metallenen Spitze durch das Spundloch quer bis zu den Rändern der beiden Böden eingeführt, und als die beiden Längen gleich gefunden worden waren, ergab die Marke am Spundloch die Zahl der Eimer im Fass.
Ich wunderte mich, dass die Querlinie durch die Fasshälfte ein Maß für den Inhalt abgeben könne und bezweifelte die Richtigkeit der Methode, denn ein sehr niedriges Fass mit etwas breiteren Böden und daher sehr viel kleinerem Inhalt könnte dieselbe Visierlänge besitzen. Es schien mir als Neuvermähltem nicht unzweckmäßig, ein neues Prinzip mathematischer Arbeiten, nämlich die Genauigkeit dieser bequemen und allgemein wichtigen Bestimmung nach geometrischen Grundsätzen zu erforschen und die etwa vorhandenen Gesetze ans Licht zu bringen.“
Im Ergebnis gelang es Kepler, ohne Kenntnisse der noch nicht entwickelten Integralrechnung ein Näherungsverfahren zur Bestimmung der Fläche unter einer Parabel zu finden. Der Name „Fassregel“ ist streng genommen nicht korrekt, da hier kein Volumen, sondern ein Flächeninhalt ermittelt wird. siehe auch Keplers Hobby (Franz von Krbek).
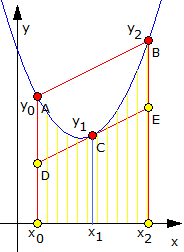 Ausgehend von drei Punkten A(x0, y0), B(x2, y2) und C(x1, y1) einer Parabel wird die Fläche im Intervall [x0, x2] in zwei Teilflächen zerlegt: zum einen in ein Trapez mit der x-Achse und der Strecke DE als Seiten und zum anderen in das Parallelogramm ABDE. Gilt
Ausgehend von drei Punkten A(x0, y0), B(x2, y2) und C(x1, y1) einer Parabel wird die Fläche im Intervall [x0, x2] in zwei Teilflächen zerlegt: zum einen in ein Trapez mit der x-Achse und der Strecke DE als Seiten und zum anderen in das Parallelogramm ABDE. Gilt
x1 = (x0 + x2)/2
so drittelt die Parabel das Parallelogramm. Diese Aussage wurde schon von Archimedes bewiesen. Somit ergibt sich für die gesuchte Fläche:
A = ATrapez + 1/3 AParallelogramm
Nach dem Einsetzen der Koordinaten entsteht die berühmte Fassregel:
A = (x2 – x0)/6 (y0 + 4 y1 + y2)
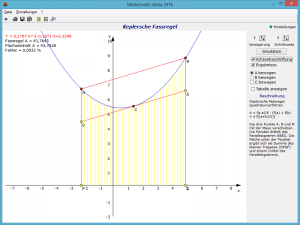
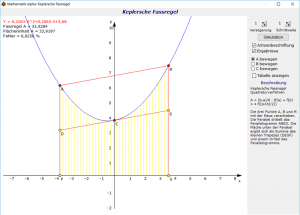
In diesem Teilprogramm können Sie die Genauigkeit der Keplerschen Fassregel mit dem exakten Integral vergleichen.
Die Punkte A, B und C sind wieder per Maus verschiebbar bzw. können auch über direkte Eingabe der Koordinaten festgelegt werden. Das Programm stellt die zugehörige Konstruktion dar und ermittelt den Flächeninhalt sowohl mit der Keplerschen Näherung als auch exakt über die Integralrechnung.
| Keplersche Fassregel |
|---|
 |
| Herunterladen |
Download von „Keplersche Fassregel“
Dieses Teilprogramm steht in vereinfachter Form als eigenständiges Programm zum Download bereit.