Komplexe Funktionen

Dieses Teilprogramm stellt komplexe Funktionen grafisch dar.
Komplexe Zahlen z = x + yi können nicht mehr auf einem Zahlenstrahl veranschaulicht werden, sondern werden nach Carl Friedrich Gauß in einer Zahlenebene dargestellt.

Ein funktionaler Zusammenhang zwischen komplexen Zahlen würde damit zur optischen Veranschaulichung einen vierdimensionalen Raum benötigen – für Argument und Funktionswert je zwei Koordinaten. Da eine Projektion des R⁴ auf eine Zeichenebene praktisch nicht möglich ist, geht man bei der Darstellung komplexwertiger Funktionen andere Wege.

Ist F(Z) = F(Re(z), Im(z)) eine Funktion in den komplexen Zahlen, so kann das Argument in der x-y-Ebene gezeichnet werden. Zusätzlich trägt man an der dritten Achse im R³ einen reellen Wert an, der den komplexen Funktionswert von Z charakterisiert. Dazu bieten sich unter anderem an

• der Realteil Re(F(Z)) der komplexen Zahl F(Z)
• der Imaginärteil Im(F(Z)) der komplexen Zahl F(Z) oder
• der Betrag |F(Z)| = √(Re²(F(Z)) + Im²(F(Z))) von F(Z)
• der Phasenplot des Funktionswertes

Die vierte Möglichkeit, die Zeichnung eines Phasenplots, wird auch im Teilprogramm Niveauflächen und Phasenplot untersucht; dort mit einer ebenen Darstellung, die wunderschöne Bilder ergibt.

Im oberen Teil dieses Teilprogramms können Sie aus einer Liste eine vordefinierte komplexe Funktion F(Z) auswählen. Diese wird in die Eingabezeile der Funktion F(Z) eingetragen. Selbstverständlich können Sie auch eine andere Funktionsgleichung eingeben.
Beachten Sie bitte, dass das Argument der Funktion Z ist und folgende Funktionen und Operanden verwendet werden können:

• Standardfunktionen SQRT, SIN, COS, TAN, COT, SEC, CSC, SINH, COSH, TANH, COTH, EXP, LN
• Spezielle Funktionen GAMMA und die Besselschen Funktionen BI0, BJ0
• Riemannsche Zetafunktion RIEMANN (Näherung bis … + 1/48^z)
• die Jacobischen elliptischen Funktion DN, SN, CN
• Exponentialintegral EI
• die Funktionen TRE(Z) und TIM(Z) für den Real- bzw. Imaginärteil des komplexen Arguments z
• Operanden +, -, *, / und die Potenzbildung ^
• Konstanten I, PI

An den Schaltfeldern wählen Sie, welcher der vier Darstellungsmodi genutzt werden soll. Die Funktionsgleichung kann einen Parameter Q enthalten. Für diesen Parameter können Sie Real- und Imaginärteil des Anfangswertes eingeben.

Betätigen Sie den Schalter Darstellung, zeichnet das Programm den Verlauf der komplexen Funktion entsprechend dem ausgewählten Wert für die F(Z)-Achse.

Die komplexwertige Funktion wird dazu innerhalb eines Koordinatenwürfels veranschaulicht. Genutzt wird die Darstellungsmöglichkeit der dreidimensionalen Funktionen F(X,Y), wobei nun Z dem ausgewählten Wert entspricht und für die Argumente X und Y der Real- bzw. Imaginärteil der komplexen Zahl eingesetzt werden.

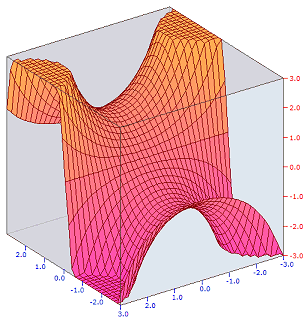Beispiel: Darstellung der komplexen Funktion F(Z) = SIN(Z), wobei längs der F(Z)-Achse der Realteil abgetragen wird.

Im unteren Teil des Programmfensters haben Sie zusätzlich die Möglichkeit, eine Wertetabelle der Funktion im Bereich der komplexen Zahlen zu berechnen.

Da innerhalb der komplexen Zahlen keine Ordnungsrelation existiert, müssen die Argumente Z getrennt nach reellem und imaginären Anteil festgelegt werden. Tragen Sie dazu in die Felder X = vier verschiedene reelle Anteile x des Arguments z = x + y i ein. Nach Betätigung des Schalters Berechnung erhalten Sie dann für alle imaginären Anteile y, deren Grenzen und Schrittweite unter Berechnung festgelegt wurden, die Funktionswerte.

Komplexe Funktionen
Herunterladen

Dieses Teilprogramm kann auch als Einzelprogramm heruntergeladen werden. Dieses besitzt aber nicht die volle Funktionalität wie in „Mathematik alpha“, u.a. ohne Kopier- und Druckfunktion.