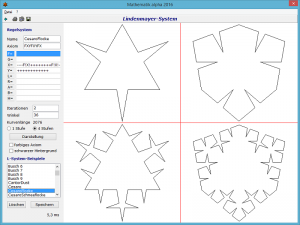
 Dieses Teilprogramm erlaubt einen Einblick in eine weitere Kategorie von Fraktalen: das L-System. Dieses System ermöglicht das Zeichnen von Fraktalen durch rekursive Definitionsgleichungen.
Dieses Teilprogramm erlaubt einen Einblick in eine weitere Kategorie von Fraktalen: das L-System. Dieses System ermöglicht das Zeichnen von Fraktalen durch rekursive Definitionsgleichungen.
In Weiterführung der Ergebnisse von J.W.Backus, P.Naur und S.Ginsburg über kontextfreie Chomsky-Grammatiken entwickelte 1968 Aristid Lindenmayer die Theorie der L-Systeme.
In „The Fractal Geometry of Nature“ von Benoit Mandelbrot wurden diese besonders durch Adrian Mariano verwirklicht. Eine Definitionsgleichung besteht aus einer Folge von Zeichen der Menge
- F , G, H, + , – , [ , ] , / , \ , <, > ! und | .
Hauptbefehl ist dabei F (für „forward“), der den eigentlichen Zeichenvorgang realisiert. Mariano nutzt darüber hinaus weitere Steuerzeichen, allerdings wird im Programm nur auf diese Grundmenge zurückgegriffen.
Die verwendete Syntax wurde in den Achtzigerjahren mithilfe der bekannten Befehle der Turtle-Grafik von S. Papert interpretiert. Dabei bedeutet:
- F … Zeichnen einer Linie
- G … Bewegen ohne Zeichnen der Linie
- H … Zeichnen einer Linie (äquivalent zu F)
- X, Y, L, R, A, B … Variablen zur Beschreibung komplexerer L-Systeme
- + … Drehung der Zeichenrichtung um einen Winkel nach oben
- – … Drehung der Zeichenrichtung um einen Winkel nach unten
- /nn … Drehung der Zeichenrichtung um den Winkel nn in Grad nach oben; nn kann als rationale Zahl mit Dezimalpunkt eingegeben werden
- \nn … Drehung der Zeichenrichtung um den Winkel nn in Grad nach unten; nn kann als rationale Zahl mit Dezimalpunkt eingegeben werden
- <nn … die Zeichenlänge wird mit dem Faktor nn/10 multipliziert
- >nn … die Zeichenlänge wird mit dem Faktor nn/10 dividiert; nn kann als rationale Zahl mit Dezimalpunkt eingegeben werden
- @xx … die Zeichenlänge wird mit der Zahl xx multipliziert
- @Ixx … die Zeichenlänge wird mit der Zahl xx dividiert; für xx müssen stets 2 (!) Ziffern eingegeben werden
- | … Drehung der Zeichenrichtung um 180°
- ! … Vertauschen der Wirkung von +,- bzw. / und \
- [ … Speichern der aktuellen Zeichenposition (PUSH)
- ] … Einstellen der zuletzt abgespeicherten Zeichenposition (POP)
- C … Änderung der Zeichenfarbe
- Anmerkung: Der Faktor nn bei den Befehlen < und > kann zwischen 01 (Faktor 0.1) und 99 (Faktor 9.9) liegen. Zur Vermeidung von numerischen Problemen ist aber bei großen Faktoren Vorsicht geboten.
Da die Definitionsgleichungen in der einfachsten Form F = f(F, G, +, -, [, ], /, \, <, >, |, !) gegeben wird, entsteht eine rekursive Vorschrift. Eine höhere Anzahl von Iterationen bewirkt ein immer stärkeres Ausbilden der typischen Fraktalform.
Die Festlegung des Drehwinkels erfolgt in ganzzahligen Anteilen des Vollwinkels, d.h., Winkel 6 bewirkt jeweils eine Drehung um 60 Grad. Im Programm ist die Anzahl der Iterationen auf den Bereich von 1 bis 10 beschränkt.
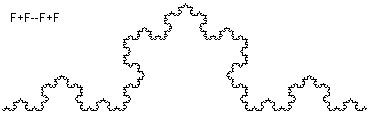 Im Beispiel wurde eine von Kochsche Kurve mit fünf Iterationen und einem Winkel von 6 (60°) gezeichnet. Die Definitionsgleichung lautet: F = F + F — F + F, d.h., nach dem Zeichnen einer Linie erfolgt eine Drehung um 60° nach oben, Zeichnen, Drehung um 120° nach unten, Zeichnen, Drehen um 60° nach oben, Zeichnen. Das Besondere an dieser Kurve und allen Kurven des L-Systems liegt in der Tatsache, dass ihr keine Bogenlänge im klassischen Sinne zugeordnet werden kann.
Im Beispiel wurde eine von Kochsche Kurve mit fünf Iterationen und einem Winkel von 6 (60°) gezeichnet. Die Definitionsgleichung lautet: F = F + F — F + F, d.h., nach dem Zeichnen einer Linie erfolgt eine Drehung um 60° nach oben, Zeichnen, Drehung um 120° nach unten, Zeichnen, Drehen um 60° nach oben, Zeichnen. Das Besondere an dieser Kurve und allen Kurven des L-Systems liegt in der Tatsache, dass ihr keine Bogenlänge im klassischen Sinne zugeordnet werden kann.
Beachten Sie bitte: Mit steigender Iterationstiefe wächst die notwendige Berechnungs- und Darstellungszeit exponentiell an. Abbrechen können Sie die Darstellung wie gewohnt durch Betätigung der ESC-Taste oder des Schalters Abbruch!
Ein Fraktal des L-Systems wird in diesem Programm im Darstellungsfenster stets so gezeichnet, dass es die volle Größe des Fensters nutzt, d.h. unabhängig von einem Koordinatensystem. In der Liste des L-Systems finden Sie rund 70 interessante Gebilde dieser Art.
Damit Sie selbst experimentieren können, besteht die Möglichkeit, Ihr eingegebenes Regelsystem in einer Bibliothek aufzubewahren.
Beachten Sie aber bei der Festlegung des Fraktals, dass Sie den Drehwinkel im Bereich 3 bis 99 wählen. Zum Abspeichern klicken Sie auf den Schalter Speichern. Tragen Sie bitte vor dem Speichern einen typischen Namen ein.
Möchten Sie einen Eintrag wieder entfernen, so markieren Sie ihn und klicken mit der rechten Maustaste auf Löschen.
Erweitertes L-System
Die Definition eines Fraktals des L-Systems ist auch über die Festlegung des Axioms und mehrerer Ersetzungsregeln möglich. Damit können noch interessantere Gebilde grafisch erzeugt werden. Zum Beispiel definiert man ein Axiom in Abhängigkeit von F, G sowie X und Y und gibt Regeln für alle Größen an. Soll die nach Hilbert benannte Kurve gezeichnet werden, setzt man:
>Axiom = X ; F = F ; X = -YF+XFX+FY- ; Y = +XF-YFY-FX+
Im Ergebnis erhalten Sie die Hilbert-Kurve.
Beachten Sie bitte, dass das Programm zur Darstellung der Kurven intern im Speicher die rekursive Ersetzung des Axioms aufbereitet. Erhöhen Sie die Rekursionstiefe, steigt zum einen die notwendige Rechenzeit (Abbruch jederzeit mit der Stopp-Taste), andernfalls kann unter Umständen der reservierte Speicher nicht ausreichen. In diesem Fall wird automatisch die vorhergehende Rekursionsstufe gezeichnet.
Darstellung mehrerer Iterationsstufen
Markieren Sie das Feld 4 Stufen, so versucht das Programm, vier aufeinander folgende Iterationen des Fraktals zu zeichnen.
Dabei müssen Sie beachten, dass zum einen die Berechnungszeit stark ansteigen und zum anderen auch die maximale Iterationstiefe überschritten werden kann.
| L-System | |
|---|---|
 |
|
| Herunterladen | |
Download
Auch dieser Programmteil kann als Einzelprogramm geladen werden.