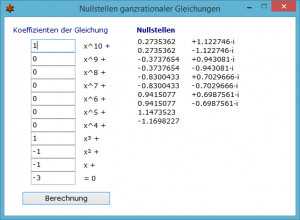
Nach dem Fundamentalsatz der Algebra besitzt eine ganzrationale Gleichung der Form
an xn + … + a3 x³ + a2 x² + a1 x + a0 = 0
stets n Lösungen im Bereich der komplexen Zahlen. Ist eine nicht reelle Zahl Lösung, so ist es auch die zugehörige konjugiert komplexe Zahl.
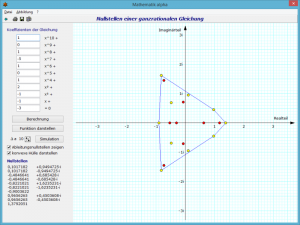In diesem Teilprogramm werden die Lösungen bis zu einem Grad n = 10 ermittelt. Dies erfolgt mit einem schnellen, speziellen Näherungsverfahren, da nur bis n = 4 exakte Lösungsformeln existieren.
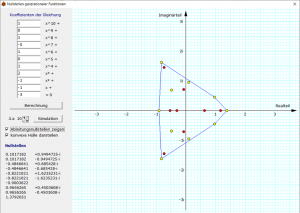
Die ermittelten Lösungen stellt das Programm in der komplexen Gaußschen Zahlenebene dar. Deutlich erkennt man, dass die reelle Achse Symmetrieachse ist.
Tragen Sie andere Koeffizienten der Gleichung ein und quittieren mit Berechnung, werden die Lösungen ermittelt.
Der Schalter Funktion darstellen ruft die grafische Darstellung auf und zeigt die zugehörige ganzrationale Funktion:
y = an xn + … + a3 x³ + a2 x² + a1 x + a0
Mit dem Schalter Simulation wird ein Koeffizient kontinuierlich verändert und das Ergebnis sofort angezeigt. Den Index des zu veränderten Koeffizienten stellen Sie an den kleinen Pfeilschaltern Δa neben dem Simulation-Schalter ein.
Gauß-Lucas-Theorem
Markieren Sie das Feld Ableitungsnullstellen anzeigen, so werden zusätzlich die komplexen Nullstellen der 1.Ableitung in rot eingezeichnet.
Nach dem Gauß-Lucas-Theorem gilt, dass alle Nullstellen der 1.Ableitung innerhalb eines konvexen Polygons in der Gaußschen Ebene liegen. Dieses Polygon ist die konvexe Hülle der Nullstellen der Ausgangsfunktion. Die konvexe Hülle kann ebenfalls dargestellt werden.
| Nullstellen ganzrationaler Funktionen |
|---|
 |
| Herunterladen |
| Nullstellen ganzrationaler Funktionen |
|---|
 |
| Herunterladen |
Download
Die Berechnung der Nullstellen, mit oder ohne die grafische Darstellung, ist auch als Einzelprogramm verfügbar.