Primzahlen

„Dass die Aufgabe, die Primzahlen von den zusammengesetzten zu unterscheiden und letztere in ihre Primfaktoren zu zerlegen zu den wichtigsten und nützlichsten der gesamten Arithmetik gehört und die Bemühungen und den Scharfsinn sowohl der alten wie auch der neueren Geometer in Anspruch genommen hat, ist so bekannt, dass es überflüssig wäre, hierüber viele Worte zu verlieren.“
Gauß 1889 in „Disquisitiones Arithmeticae“

Primzahl-Definition
Eine ganze Zahl p>1 heißt Primzahl genau dann, wenn sie genau 2 Teiler besitzt, nämlich sich selbst und 1. Primzahlen werden auch irreduzible Zahlen genannt. Die Eigenschaft Primzahl zu sein, wird oft auch mit „die Zahl ist prim“ ausgedrückt.
Die Eins ist nach Definition keine Primzahl!

Aus dem Griechischen πρωτος αριθμος wörtlich übersetzt, bedeutet Primzahl „erste Zahl“. 1202 verwendete Fibonacci den Begriff „nichtzusammengesetzte Zahl“, der sich aber nicht durchsetzen konnte.
Neben zahlentheoretischen Untersuchungen erhalten diese Zahlen immer stärkere Bedeutung, da mit Hilfe besonders großer Primzahlen schwer zu entschlüsselnde Codierungen aufgebaut werden können.

Beispiele für große Primzahlen: 10⁵⁰⁶ – 10²⁵³ – 1, 2^2976221 – 1 und 2^1398269 – 1

Titan-Primzahl:Ein Titan-Primzahl ist eine Primzahl mit mehr als 1000 Ziffern (nach Yates).
Gigant-Primzahl: Eine Gigant-Primzahl ist eine Primzahl mit mehr als 10000 Ziffern.

Merkwürdige Primzahlen sind zum Beispiel
Ziffernfolge: 123456789 siebenmal hintereinander und die Ziffern 1234567
10⁵⁰⁶ – 10²⁵³ – 1 = 999…9998999…999
Die einzige gerade Primzahl ist 2.

Schon Euklid von Alexandria (um 365-300 v.u.Z.) bewies, dass unendlich viele Primzahlen existieren müssen. Im Buch VII der „Elemente“ begründet Euklid auch die Bezeichnung πρωτος αριθμος (lateinisch: numerus primus; englisch: prime number; französisch: nombre premier; deutsch: erste Zahl) indem er alle anderen Zahlen als aus Primzahlen, den ersten, grundlegenden Zahlen, zusammengesetzt erklärt.

Primzahlen-Geschichte
Primzahlen wurden schon auf Kerbhölzern aus Knochen der Altsteinzeit gefunden.
Die Knochen von Ishango stammen aus dem Jungpaläolithikum, dem jüngeren Abschnitt der Altsteinzeit, d.h. einen Zeitraum von 18000 bis 20000 v.u.Z.
Es handelt sich um Pavian-Knochen. 1960 fand diese Knochen der Belgier Jean de Heinzelin de Braucourt in Belgisch-Kongo, im Grenzgebiet zu Uganda. Sicher ist, dass in der Altsteinzeit in dieser Region eine weit entwickelte Zivilisation vorhanden war, die durch einen Vulkanausbruch ausgelöscht wurde.

Das Überraschende ist, dass die Knochen 3 Reihen von Kerben ausweisen, die jeweils in Gruppen angeordnet sind.
Die erste Reihe besteht aus 4 Gruppen zu 19, 17, 13 und 11 Kerben. Die zweite Reihe ist nicht klar zu entziffern, die dritte zeigt die Zahlen 9, 19, 21 und 11; erneut in der Summe 60.

Allein die Tatsache, dass vor 23000 Jahren Zahlen durch Markierungen gekennzeichnet wurden, ist verblüffend. Dass aber in der ersten Reihe ausschließlich Primzahlen auftreten, führte unter Archäologen zu Spekulationen. Es gibt bis heute keine wissenschaftliche Erklärung. Die Ishango-Knochen befinden sich heute im Königlichen Belgischen Institut für Naturwissenschaften in Brüssel.

Primzahlbegriff in Euklids „Elementen“
Im ersten der drei Bücher zur Arithmetik (Buch VII-IX) der „Elemente“ gibt Euklid mehrere Definitionen:

Definition 1: Einheit ist das, wonach jedes Ding eines genannt wird.
Definition 2: Zahl ist die aus Einheiten zusammengesetzte Menge.
Definition 3: Primzahl ist eine Zahl, die sich nur durch die Einheit messen lässt.

Damit ist die 1 für Euklid keine Zahl, sondern eben die „Einheit“. Als besonders sieht er außerdem die Primzahlen („ersten Zahlen“) an.
Durch Nikomachos wurde die Einteilung Einheit-Primzahl-nicht Primzahl erweitert, indem er die geraden Zahlen in vollkommene (Vollkommene Zahlen), in überschießende (abundante Zahlen) und in mangelhafte (defiziente Zahlen)
einteilte.
Die ungeraden Zahlen wurden in die Klassen Primzahlen, relativ prime Zahlen und zusammengesetzte Zahlen unterschieden. Dabei verstand Nikomachos unter den relativ primen Zahlen solche, welche zwar nicht prim sind aber nur einen Primfaktor besitzen, d.h. also alle Potenzen von Primzahlen.
Zusammengesetzte Zahlen sind nach seiner Meinung nur die, welche mindestens zwei Primteiler aufweisen. Diese Zahlen nennt er „zweite Zahlen“ (δευτερος αριθμος, numerus secundus).

Primzahlbeweis in Euklids „Elementen“
Im Buch IX, 20 führt Euklid seinen historischen Beweis zur Unendlichkeit der Primzahlen. In deutscher Übersetzung lautet er:

Es gibt mehr Primzahlen, als jede vorgelegte Anzahl von Primzahlen.
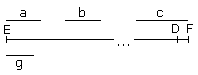Die vorgelegten Primzahlen seien a, b, c. Ich behaupte, dass es mehr Primzahlen gibt als a, b, c.
Man bilde zunächst die kleinste von a, b, c gemessene Zahl (VII, 36); sie sei DE, und man füge zu DE die Einheit DF hinzu. Entweder ist EF dann eine Primzahl, oder nicht. Zunächst sei es eine Primzahl. Dann hat es mehr Primzahlen als a, b, c gefunden, nämlich a, b, c, EF.

Zweitens sei EF keine Primzahl. Dann muss es von irgendeiner Primzahl gemessen werden (VII, 31); es werde von der Primzahl g gemessen. Ich behaupte, dass g mit keiner der Zahlen a, b, c zusammenfällt. Wenn möglich tue es dies nämlich. a, b, c messen nun De; auch g müsste dann DE messen. Es misst aber auch EF. g müsste also auch den Rest, die Einheit DF messen, während es eine Zahl ist; dies wäre Unsinn.
Also fällt g mit keiner der Zahlen a, b, c zusammen; und es ist Primzahl nach Voraussetzung. Man hat als mehr Primzahlen als die vorgelegte Anzahl a, b, c gefunden, nämlich a, b, c, g.

Primzahlen der Form 1000…000z

Für den Bereich 0 < n < 15587 (März 2019, Polster) wurden alle Zahlen der Form 10ⁿ+z mit z = 3, 7, 9, 13, 19, 21, 27, 31 bzw. 33 auf Primzahleigenschaft getestet. Primzahlen wurden gefunden für …

	endend auf n …
1	1, 2
3	1, 2, 5, 6, 11, 17, 18, 39, 56, 101, 105, 107, 123, 413, 426, 2607, 7668, 10470, 11021, 17753, 26927
7	1, 2, 4, 8, 9, 24, 60, 110, 134, 222, 412, 700, 999, 1383, 5076, 5543, 6344, 14600, 15093, 21717, 23636, 30221, 50711
9	1, 2, 3, 4, 9, 18, 22, 45, 49, 56, 69, 146, 202, 272, 2730, 2841, 4562, 31810, 43186, 48109

Die größte, durch den Autor gefundene, derartige Primzahl 10¹⁵⁰⁹³+7 besteht damit aus einer Ziffer ‚1‘, 15092 Ziffern ‚0‘ und einer Ziffer ‚7‘.
Weiterhin enden Primzahlen der Form 10ⁿ+z auf z = 13, 19, 21, 27, 31 bzw. 33:

	endend auf n …
13	2, 3, 17, 25, 81, 140, 142, 152, 280, 291, 406, 4209, 4785, 8474, 9550, 9596
19	3, 5, 7, 10, 11, 17, 59, 81, 108, 574, 629, 1069, 1759, 2063, 2682, 9174
21	1, 3, 9, 17, 55, 77, 133, 195, 357, 1537, 2629, 3409, 8007
27	1, 2, 83, 167, 242, 14081
31	1, 2, 3, 14, 18, 44, 54, 89, 469, 2060, 2985, 6197
33	1, 3, 6, 9, 10, 31, 47, 70, 281, 366, 519, 532, 775, 1566, 1627, 2247, 2653, 4381, 4571, 13239, 15393

Im Englischen werden Primzahlen der Form 10ⁿ ± z Randprimzahlen genannt. Ist z < n so wird die Primzahl defiziente Randprimzahl genannt, für z = n effiziente Primzahl und für z > n suffiziente Randprimzahl.

Primzahlen der Form bⁿ+1

Primzahlen der Form bⁿ + 1 können für Basen b = 2, 4, 6, … nur auftreten, wenn n eine Zweierpotenz ist. Andernfalls ist bⁿ + 1 zusammengesetzte Zahl.
Für b = 2 ergeben sich die Fermatschen Primzahlen. Man kennt nur fünf Primzahlen dieser Art
2¹ + 1 = 3 ; 2² + 1 = 5 ; 2⁴ + 1 = 17 ; 2⁸ + 1 = 257 und 2¹⁶ + 1 = 65537

Für die Basis 10 kennt man bisher nur die Primzahlen
10¹ + 1 = 11 und 10² + 1 = 101
Für andere Zweierpotenzen als Exponenten findet man die Zerlegung
10⁴ + 1 = 73 · 137
10⁸ + 1 = 17 · 5882353
10¹⁶ + 1 = 353 · 449 · 641 · 1409 · 69857
10³² + 1 = 19841 · 976193 · 6187457 · 83442 74065 78561
10⁶⁴ + 1 = 1265011073 · 153 43168 18888 91378 18369 · 515 21752 52652 13267 44786 99068 15873
10¹²⁸ + 1 = 257 · 15361 · 453377 · P116
10²⁵⁶ + 1 = 10753 · 8253953 · ???
10⁵¹² + 1 = 302078977 · ???