Die Quaternionen werden auch Hamilton-Zahlen genannt.
Die Quaternionen bilden eine Erweiterung der komplexen Zahlen. Statt einer imaginären Einheit i gibt es drei (i, j, k), so dass ein Quaternion eine Zahl der Form a + b·i + c·j + d·k ist.
Die Addition von Quaternionen ist wie bei den komplexen Zahlen komponentenweise definiert. Hamilton hatte lange Zeit nach einer geeigneten Multiplikation gesucht:
| i² = j² = k² = -1 i·j = k ; j·k = i ; k·i = j j·i = -k ; k·j = -i ; i·k = -j |
Diese Multiplikation ist nicht kommutativ.
In Mathematik und Physik gibt es Anwendungen der Quaternionen, aber sie haben nicht die Bedeutung erlangt, die Hamilton ihnen vorhergesagt hat. Ein aktuelles Anwendungsbeispiel sind 3D-Rotationen. Diese lassen sich mit Quaternionen beschreiben, wovon in der Computergrafik Gebrauch gemacht wird.
 Die Entdeckung der Quaternionen durch Hamilton ist legendär.
Die Entdeckung der Quaternionen durch Hamilton ist legendär.
Täglich führte der Weg William R.Hamilton an der Brougham Bridge vorbei, die heute Broombridge heißt. An dieser Stelle hatte Hamilton die entscheidende Idee. Er fand geeignete Multiplikationsregeln für die Quaternionen und ritzte diese mit einem Taschenmesser in einen Stein der Brücke. Leider sind die Zeichen längst verwittert. An der Brücke ist eine Gedenktafel angebracht.
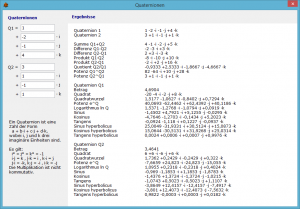
In diesem Teilprogramm werden einfache Berechnungen mit Quaternionen durchgeführt.
Nach der Eingabe der Komponenten a, b, c und d zweier Quaternionen werden diese mit elementaren Operationen verknüpft sowie Funktionswerte berechnet, u.a. die Quadratwurzel, der Logarithmus, trigonometrische Werte usw.
| Quaternionen | |
|---|---|
 |
|
| Herunterladen | |
Download
Der Programmteil zur Berechnung von Quaternionen existiert auch als einzelnes Programm. Downloadmöglichkeit: