 Das Prinzip des logarithmischen Rechenstabes wurde um 1620 von dem englischen Mathematiker Edmund Gunter entwickelt. Grundlage waren die Arbeiten von Bürgi und Napier zu den Logarithmen.
Das Prinzip des logarithmischen Rechenstabes wurde um 1620 von dem englischen Mathematiker Edmund Gunter entwickelt. Grundlage waren die Arbeiten von Bürgi und Napier zu den Logarithmen.
Der Rechenstab Gunters, die so genannte „Gunter-Skala“, basierte auf Logarithmen zur Basis 10. Durch Anwenden der Logarithmengesetze führte Gunter die Multiplikation auf die Addition von Strecken und die Division auf die Subtraktion von Strecken zurück. Die Längen wurden mithilfe eines Stechzirkels abgetragen.
Wingate und Partridge konstruierten Rechenstäbe mit einer Zunge, die in einem Stabkörper gleitet. Ende des 19. Jahrhunderts erhielt der Rechenstab durch den französischen Mathematiker Mannheim zwei Hauptskalenpaare und einen Läufer.
Der Rechenstab besteht aus dem Körper, dem Schieber, auch Zunge genannt, und dem Läufer. Die Zunge lässt sich im Körper verschieben. Der Läufer mit seiner Strichmarke kann über Zunge und Stab bewegt werden.
Auf Stabkörper und Zunge befinden sich Skalen:
Auf dem Körper die Skalen K für die Kubikzahlen, A für Quadratzahlen, die Grundskala D sowie die linear geteilte Skala L, auf der Zunge ist eine zweite Grundskala C, eine zweite Skala B der Quadratzahlen und eine Skala R der zur Skala C reziproken Werte (Kehrwerte).
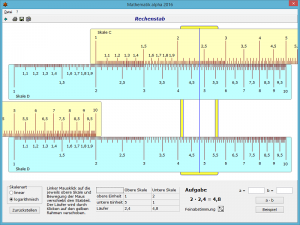
In diesem Teilprogramm können Sie einen solchen Rechenstab untersuchen. Dargestellt werden die Skalen C und D, die für die Multiplikation verwendet werden, und der Läufer zum genauen Einstellen und Ablesen der Werte.
Die beiden Skalen sind zweimal vorhanden, um die Multiplikation mit Rückschlag der Zunge zu vermeiden.
Ein linker Mausklick auf die Skala C und anschließendes Bewegen der Maus verschiebt die Zunge. Der Läufer wird analog verschoben. Dazu ist sein gelber Rand anzuklicken.
Eine Feinabstimmung ist mit den zwei kleinen Schaltern im unteren rechten Fensterteil möglich.
Ein Doppelklick auf das Fenster blendet den unteren Fensterteil ein und aus, so dass auch nur der Rechenstab angezeigt werden kann.
Multiplikation mit dem Rechenstab
Die Multiplikation wird auf der Grundlage des Logarithmengesetzes
lg (ab) = lg a + lg b
ausgeführt. Die Addition der beiden Logarithmen erfolgt am Rechenstab als Addition zweier Strecken der Länge lg a und lg b.
Dazu stellt man die Zahl 1 der Zungenskala C über die Zahl a von Skala D. Dann wird der mittlere Teilstrich des Läufers auf Zahl b der Skala C eingestellt und darunter auf Skala D das Produkt a·b abgelesen.
Stellt man den Rechenstab ein, kann das Produkt unter Umständen außerhalb der Skala D liegen und nicht mehr abgelesen werden. In diesem Fall wird nicht der Skalenanfang 1, sondern durch Verschieben der Zunge nach links der Endwert 10 von Skala C über die Zahl a von Skala D eingestellt. Wie immer wird dann der Läufer über den zweiten Faktor b eingestellt und das Produkt darunter auf Skala D abgelesen. Diese Rechenart wird Multiplikation mit Rückschlag genannt.
Da die Zahlenwerte immer nur als Ziffernfolge, also ohne Berücksichtigung der Dezimalstellen, eingegeben und auch abgelesen werden, ist eine Überschlagsrechnung zur Ermittlung der Stellenzahl notwendig.
Division mit dem Rechenstab
Zugrunde liegt hier das Logarithmengesetz
lg (a/b) = lg a – lg b
Am Rechenstab muss also von einer Strecke der Länge lg a eine Strecke der Länge lg b subtrahiert werden. Dazu wird die Zahl b der Zungenskala C über die Zahl a der Skala D geschoben. Der Läufer kann hier als Einstellhilfe dienen. Unter dem Anfangswert 1 von Skala C wird der Quotient a / b abgelesen.
Der logarithmische Rechenstab war bis Mitte der Achtzigerjahre des 20. Jahrhunderts ein wichtiges Rechenhilfsmittel, das erst mit der Entwicklung des elektronischen Taschenrechners verdrängt wurde.
Additionsrechenstab
Die Idee des Rechnens durch das Aneinanderfügen von Strecken kann auch zur Addition genutzt werden.
Wählen Sie unter Skalenart den Eintrag linear aus, so werden nicht logarithmisch, sondern linear geteilte Skalen angezeigt. Durch Verschieben der Zunge ist damit die Addition und die Subtraktion von Zahlen möglich.
Der Additionsrechenstab konnte sich nie richtig durchsetzen, da die schriftliche Addition und Subtraktion einfach und schneller zu absolvieren waren.
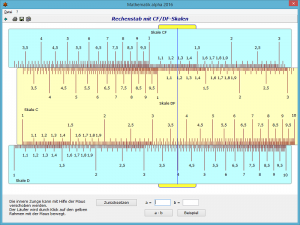 Rechenstab mit CF/DF-Skalen
Rechenstab mit CF/DF-Skalen
In einem zweiten Teilprogramm wird ein Rechenstab demonstriert, der über den Skalen C und F die CF- und DF-Skale aufweist. Diese Skalen sind um den Faktor π verschoben.
Damit kann man Multiplikationen und Divisionen, die durch einen Überlauf einen Rückschlag benötigen, ohne diesen Rückschlag durchführen. Dazu wird die Berechnung statt auf den klassischen C/D-Skalen auf CF und DF durchgeführt.
| Rechenstab und Rechenstab mit CF/DF-Skalen |
|---|
 |
| Herunterladen |
Auch hier kann mit einem linken Mausklick auf die Skala C und anschließendes Bewegen der Maus die Zunge verschoben werden. Der Läufer wird analog verschoben. Dazu ist sein gelber Rand anzuklicken.
Download
Der Rechenstab und der Stab mit den CF/DF-Skalen stehen als eigene Programme zum Download zur Verfügung.