Zur Konstruktion sozialer, befreundeter und geselliger Zahlen wird die Teilersumme aller echter Teiler und der Zahl 1 einer natürlichen Zahl n gebildet.
Ist a2 die Teilersumme von a1, a3 die von a2, …, und a1 die von ar, so bildeten diese r Zahlen eine r-gliedrige Kette von sozialen Zahlen.
Ist die Länge r=2 liegen befreundete Zahlen vor, für r=1 ist die Zahl vollkommen. Interessant ist nun, die Folge dieser Teilersummen zu betrachten. Für n = 30 ergibt sich
42, 54, 66, 78, 90, 144, 259, 45, 33, 15, 9, 1
d.h. die Folge endet bei 1.
Bei Untersuchung der ersten natürlichen Zahlen zeigt sich nun, dass
- die Folge nach Erreichen einer Primzahl anschließend bei 1 endet
- die Folge zyklisch wird (vollkommene, befreundete oder gesellige Zahlen oder in der Teilersumme treten solche Zahlen auf)
- das Verhalten der Folge noch nicht bekannt ist, evtl. wächst die Folge über alle Grenzen, sie divergiert
Zu vermuten ist, dass der 3.Fall, stets in den ersten oder zweiten einmündet. Da es wesentlich mehr defiziente als abundante Zahlen gibt, ist eine divergente Teilersummenfolge unwahrscheinlich.
Allerdings ist diese Vermutung, die Catalan-Dickson-Vermutung, heute noch nicht bewiesen. Derartige Folgen, deren Verhalten noch nicht bekannt ist, werden Offenendketten genannt. Startzahlen, welche bei der gleichen Primzahl enden, werden Primzahlfamilie genannt.
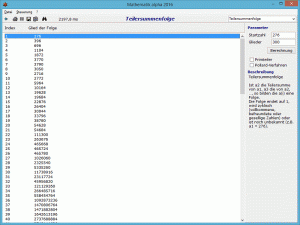
In diesem Programm wird nach derartigen Teilersummenfolgen gesucht. Tragen Sie dazu die Startzahl und die Anzahl der Folgenglieder ein.
Zur Berechnung ist die vollständige Faktorisierung der Folgenglieder notwendig. Insbesondere für Zahlen ab 20 Stellen ist dies aufwendig. Hier werden nach Probedivisionen das Brent-Rho-Verfahren (auf Wunsch auch das etwas langsamere Pollard-Rho-Verfahren) und die Faktorisierung mit elliptischen Kurven verwendet.
Beachten Sie bitte, dass die Faktorisierung ein sehr aufwendiger Prozess ist, der durchaus längere Zeit benötigt. Abbrechen können Sie jederzeit über den Schalter.
Die Berechnung stoppt automatisch, wenn die 1 oder die Startzahl erreicht wird. Unter Umständen ist die Primteilersuche zu aufwendig. In diesem Fall bricht das Programm automatisch ab.
Insbesondere tritt dies für Startzahlen, die zu den Lehmer-Five gehören, ein.
Für diese Startzahlen ist bis heute nicht bekannt, wie die Folge endet. Die kleinste dieser Zahlen ist die 276.
Immerhin gelingt es hier, für die 840 die vollständige Folge mit 748 Gliedern zu berechnen.
| Teilersummenfolge | |
|---|---|
|
|
| Herunterladen | |
Download
Dieses Teilprogramm kann auch als eigenständiges Programm geladen werden. Dabei ist zu beachten, dass das Einzelprogramm nicht die volle Funktionalität besitzt, wie im Projekt „Mathematik alpha“.