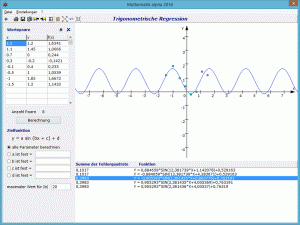
 In diesem Teilprogramm können Sie eine weitere Variante der nichtlinearen Regression nutzen, die „Trigonometrische Regression“.
In diesem Teilprogramm können Sie eine weitere Variante der nichtlinearen Regression nutzen, die „Trigonometrische Regression“.
Gegeben ist ein Menge von Wertepaaren (xi, yi) und die trigonometrische Funktion
f(x) = a sin (bx + c) + d
Ziel ist es, die Parameter der Funktion so zu bestimmen, dass diese möglichst gut die Menge von Wertepaaren approximiert, d.h. mit möglichst minimaler Fehlerquadratsumme
Σ (f(xi) – yi)²
Für die Berechnung ermittelt man partielle Ableitungen
ga(x) = sin (bx+c) · Δ a
gb(x) = ax cos (bx+c) · Δ b
gc(x) = a cos (bx+c) · Δ c
gd(x) = Δ d
wobei a, b, c, d die konkreten Näherungswerte darstellen. Δa, Δb, Δc und Δd sind noch zu bestimmende Koeffizienten der Linearkombination
g(x) =a sin (bx+c) + d + sin(bx + c) · Δ a+ ax cos (bx + c) · Δ b + a cos (bx + c) · Δ c + Δ d
Diese Koeffizienten (Δa, Δb, Δc, Δd) werden mit dem Gaußschen Algorithmus der kleinsten Quadrate nun so berechnet, dass die Fehlerquadratsumme
σ² = Σ (yi -g(xi))²
minimal wird. Bessere Näherungen für die Parameter a bis d ergeben sich durch
a ⇒ a + Δ a , b ⇒ b + Δ b
usw. Mehrere Wiederholungen des Verfahrens ergeben eine günstige Lösung.
Tragen Sie zur Auswertung x- und y-Werte in die Wertepaartabelle ein oder laden Sie diese von der Festplatte. Klicken Sie auf den Schalter Berechnung, ermittelt das Programm die Parameter.
Im Gegensatz zu anderen Regressionsverfahren existiert hier keine eindeutige Lösung. So zeigt sich, dass für höhere Koeffizienten b meist Lösungen mit kleiner Fehlerquadratsumme gefunden werden.
Zusätzlich kann der Parameter c natürlich noch durch Addition der Periodenlänge verändert werden.
Die gefundenen Koeffizienten hängen sehr stark von den gewählten Startparametern ab. Aus diesem Grund berechnet das Programm zehnmal die Koeffizienten für andere Startwerte und trägt die gefundenen Funktionen in die Liste ein.
Möchten Sie eine dieser Funktionen anzeigen, so wählen sie diese in der Liste aus.
Voreingestellt werden alle vier Parameter a bis d berechnet. Kennen Sie einen der vier, so können Sie das Feld xx fest markieren und den Wert eintragen.
Bei einer Berechnung wird dann dieser Koeffizient unverändert gelassen.
| Trigonometrische Regression | |
|---|---|
 |
|
| Herunterladen | |
Download
Dieser Programmteil existiert auch als einzelnes Programm, allerdings in einfacherer Form als im Programmpaket „Mathematik alpha“.