1936 wurde von dem englischen Mathematiker Alan M. Turing das Modell einer Maschine erdacht, mit der jeder berechenbare Algorithmus bearbeitet werden kann. Die Besonderheit der Turing-Maschine besteht darin, dass seit ihrer Erfindung kein berechenbarer Algorithmus, und sei er noch so kompliziert, gefunden wurde, der nicht auf ihr berechnet werden kann. Heute geht man davon aus, dass die Curchsche These:
Jeder Algorithmus kann durch eine Turing-Maschine realisiert werden.
richtig ist, womit jede Turing-Maschine ebenso mächtig wie alle unsere Personalcomputer oder auch Supercomputer ist. Zu beachten ist dabei, dass zum einen nicht jedes Problem algorithmisierbar ist, zum anderen eine Berechnungsvorschrift auf Turing-Maschinen auch für an sich einfache mathematische Aufgaben sehr umfangreich und kompliziert sein kann. Eine Turing-Maschine besteht aus folgenden Teilen:
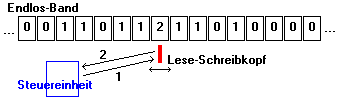 • Einem unendlich langen Band. Dieses Band besteht aus Zellen. Jede Zelle speichert genau ein Zeichen. Diese Zeichen entstammen einem Bandalphabet A, im Programm: A = {0,1,2,3,4}
• Einem unendlich langen Band. Dieses Band besteht aus Zellen. Jede Zelle speichert genau ein Zeichen. Diese Zeichen entstammen einem Bandalphabet A, im Programm: A = {0,1,2,3,4}
• Einem Lese-Schreibkopf. Er kann jeweils genau ein Zeichen vom Band lesen bzw. auf das Band schreiben. In jedem Takt bewegt er sich genau eine Zelle nach links oder rechts bzw. bleibt an der gleichen Stelle stehen. Die Menge der Bewegungen ist damit {L,R,S}.
• Einem Leitwerk. Dieses Leitwerk steuert die Arbeit des Lese-Schreibkopfes. Im Leitwerk ist das Programm (die Turing-Tafel) gespeichert. Das Leitwerk befindet sich ständig im aktuellen Zustand und kann diesen entsprechend dem Programm ändern. Die Menge aller Zustände sei Z.
Zu Beginn befindet sich das Leitwerk im Zustand Z0. Folgende Schrittfolge steuert die Maschine:
• Lesen des Zeichens auf dem Band, z.B. 1
• Lesen der Turing-Tafel für den Zustand Z0, z.B. [ 0,0,S | 0,1,R | 2,0,S | 3,0,S ]
• Bestimmung des Befehls entsprechend des Zeichens, im Beispiel neues Zeichen = 0, neuer Zustand = Z1, Bewegung nach R
• Eintragen des neuen Zeichens, im Beispiel 0
• Ausführung der Bewegung, im Beispiel eine Zelle nach rechts
• Beginn bei 1. mit neuem Zustand, im Beispiel Z1
Die hier in „Mathematik alpha“ implementierte Turing-Maschine, eine deterministische Ein-Band-Maschine, stoppt, wenn erneut der Zustand Z0 erreicht wird. Entsprechend der beschriebenen Arbeitsweise sind folgende Überlegungen und Eingaben vorzunehmen:
• Festlegung der Anzahl der Zustände, maximal 0 … 9
• Festlegung des Bandalphabets, maximal 0, 1, 2, 3, 4
• Je Zustand sind je Zeichen in das entsprechende Feld „Neues Zeichen, Neuer Zustand, Bewegung“ (mit Komma getrennt) einzugeben
Beispiel:
| Zeichen | 0 | 1 | 2 | 3 |
| Zustand Z0 | 0,0,S | 0,1,R | 2,0,S | 3,0,S |
| Zustand Z1 | 1,2,R | 1,1,R | 2,1,S | 3,1,S |
| Zustand Z2 | 0,5,L | 2,3,L | 2,2,R | 3,2,R |
| Zustand Z3 | 0,4,R | 3,2,R | 2,3,L | 3,3,L |
| Zustand Z4 | 0,2,L | 1,2,L | 1,4,R | 0,4,R |
| Zustand Z5 | 0,6,R | 1,2,R | 0,5,L | 1,5,L |
| Zustand Z6 | 0,0,S | 1,6,R | 2,6,S | 3,6,S |
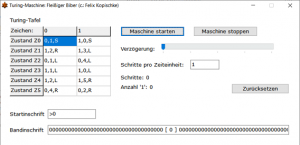
Zusätzlich geben Sie unter Bandinschrift die Anfangsbelegung des Bandes ein. Mit > kennzeichnen Sie die Position des Startzustands. Nach Betätigung der RETURN-Taste bzw. des Schalters Start der Turing-Maschine arbeitet die Turing-Maschine. Sie erhalten als Anzeige die aktuelle Belegung des Bandes in der Nähe des aktuellen Zustands, die Anzahl der abgelaufenen Schritte und die Anzahl der Zeichen ‚1‘, ‚2‘, ‚3‘ und ‚4‘ auf dem ganzen Band. In Anzeige nach … Schritten geben Sie an, nach wie vielen Schritten die Anzeige aktualisiert wird. Unter Verzögerung können Sie einen Wert von 0 bis 30000 wählen, der eine Zeitschleife in Millisekunden angibt, die nach jedem Schritt eingefügt wird. Dieser Wert ermöglicht es Ihnen, den Lauf der Turing-Maschine Schritt für Schritt zu verfolgen.
Beispiel: Geben Sie für die oben angegebene Turing-Tafel die Startinschrift >111111011111111 ein, so ermittelt diese Turing-Maschine den größten gemeinsamen Teiler von 6 und 8 und stoppt nach 164 Schritten mit der Bandinschrift 2.
| Turing-Maschine | |
|---|---|
 |
|
| Herunterladen | |
Download
Eine spezielle Version einer Turing-Maschine kann hier als Einzelprogramm geladen werden. Diese Turing-Maschine simuliert einen „fleißigen Biber“, einen Automaten, der möglichst viele Einsen auf das Band schreibt und die nach einer endlichen Anzahl Rechenschritte den Halt-Zustand annimmt.
Die ZIP-Datei enthält neben der Exe-Datei auch den Quelltext.
Dieses Programm wurde von Felix Kopischke erstellt. Danke für die Zustimmung zur Veröffentlichung.