 1883 erfand der französische Mathematiker Edouard Lucas das bekannte Problem der Türme von Hanoi (auch nur Turm von Hanoi) und machte es in Form eines Spiels allgemein bekannt. Dabei berichtete er von einer Legende:
1883 erfand der französische Mathematiker Edouard Lucas das bekannte Problem der Türme von Hanoi (auch nur Turm von Hanoi) und machte es in Form eines Spiels allgemein bekannt. Dabei berichtete er von einer Legende:
„In der Stadt Hanoi stehen in einem Brahma-Tempel drei Säulen. Auf einer dieser Säulen liegen 64 Scheiben, die, von oben nach unten gesehen, einen streng monoton wachsenden Durchmesser haben. Die Welt wird in Schutt und Asche fallen, wenn die Mönche die Scheiben der ersten Säule auf eine andere Säule gelegt haben. Dabei darf nie mehr als 1 Scheibe gleichzeitig bewegt und niemals eine größere Scheibe auf eine kleinere gelegt werden …“
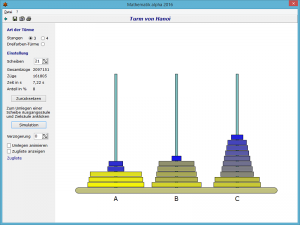
Im Programm ist dieses Problem unter diesem Programmpunkt wie folgt umgesetzt:
Der Turm von Hanoi besteht aus drei Säulen, auf die Scheiben unterschiedlicher Radien gesteckt werden können. Ziel ist es, den Turm von links nach rechts zu transportieren, wobei entsprechend der Legende folgende zwei Regeln zu beachten sind:
- bei jedem Zug darf nur eine Scheibe bewegt werden.
- eine Scheibe darf nur auf eine andere Scheibe gelegt werden, wenn diese einen größeren Radius hat
An den Rollbalken und Schaltfeldern können Sie folgende Einstellungen vornehmen:
- die Scheibenzahl von 3 bis 36 Scheiben
- eine Verzögerungszeit der Darstellung von 0 bis 20
Eine Scheibe bewegen Sie, in dem Sie zuerst auf den Ausgangsstab mit der Maus klicken und anschließend auf den Zielstab. Jeder Zug wird gezählt und angezeigt.
Wenn Sie optimale Lösung finden, so haben Sie am Ende genau so viele Züge benötigt, wie unter Gesamtzüge angezeigt.
Betätigen Sie nun den Simulation-Schalter, beginnt das Programm mit der Bewegung der Scheiben. Diese Simulation kann jederzeit mit der ESC-Taste abgebrochen werden.
Während die Scheibenzahl die notwendigen Scheibenbewegungen festlegt, bewirkt die Verzögerung eine langsamere oder schnellere Animation. Je höher dieser Wert ist, desto langsamer wird das Programm die Scheiben bewegen.
Wählen Sie das Feld Umlegen animieren aus, so wird das Umlegen jeder Scheibe langsam vorgeführt.
Markieren Sie das Feld Zugliste anzeigen, so trägt das Programm die Zugfolge in eine Liste ein.
Übrigens: Da die Anzahl der notwendigen Bewegungen bei n Scheiben 2n – 1 beträgt, müssen die Mönche in Hanoi 18 Trillionen 446 Billiarden 744 Billionen 73 Milliarden 709 Millionen und 551615 mal eine Scheibe transportieren. Benötigen sie für jede Bewegung genau 1 Sekunde, schlafen nicht, essen nicht usw., so sind alle Scheiben nach etwa 585 Milliarden Jahren umgelegt. Da das gesamte Weltall erst 14 Milliarden Jahre existiert und unsere Sonne in etwa 5 Milliarden Jahre erlischt, brauchen wir uns über den Weltuntergang durch die Türme von Hanoi wahrlich keine Gedanken zu machen.
Auf einem 2,6 GHz-Testrechner wurden ohne(!) grafische Darstellung 6 Millionen Umlagerungen je Sekunde berechnet. Für die 64 Scheiben benötigt dieser Computer also rund 100000 Jahre. Auch dieser Zeitabschnitt ist unvorstellbar groß.
Mit einer Animation der Scheiben (ohne Verzögerung) wurden für 20 Scheiben 35 s benötigt. Für 36 Scheiben wären dies rund 2,3 Millionen Sekunden, d.h. über 26 Tage! Wahrscheinlich wird kein Nutzer dieses Programmteils die maximal 36 Scheiben wirklich umlegen lassen. Die reine Berechnung der Verschiebungen benötigt für 36 Scheiben schon über 4 Stunden!
Vierstangen-Turm von Hanoi
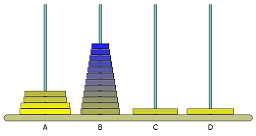 Eine interessante Variante des Turms von Hanoi ist die analoge Problemstellung mit vier statt drei Stangen. Steht die vierte Stange zur Verfügung, so verringert dies die Anzahl der notwendigen Züge für höhere Scheibenzahlen erheblich.
Eine interessante Variante des Turms von Hanoi ist die analoge Problemstellung mit vier statt drei Stangen. Steht die vierte Stange zur Verfügung, so verringert dies die Anzahl der notwendigen Züge für höhere Scheibenzahlen erheblich.
Durch Herrn Dr. Wolfang Schöbel wurde ein Verfahren zur Ermittlung der Anzahl der kürzesten notwendigen Zugzahlen gefunden. Hier steht diese Herleitung zur Verfügung. Vielen Dank.
Daraus ergeben sich folgende Zugzahlen als die kleinsten für n = 1, 2, 3, … Scheiben:
1, 3, 5, 9, 13, 17, 25, 33, 41, 49, 65, 81, 97, 113, 129, 161, 193, 225, 257, 289, …
Zur programmtechnischen Lösung wird der empirische Frame-Stewart-Algorithmus verwendet, dessen optimale Strategie bis 30 Scheiben nachgewiesen wurde. Gegeben sind n Scheiben:
1) für eine Anzahl k, werden die obersten k Scheiben auf einen zweiten Stab transportiert unter Ausnutzung aller 4 Stäbe
2) die verbliebenen n-k Scheiben werden von der 1. Stange zur 4. bewegt ohne Berücksichtigung der belegten 2.Stange.
3) die k Scheiben der 2. Stange werden unter Nutzung aller 4 Stangen zur 4. verschoben.
Die Schwierigkeit besteht darin, dass das k so gewählt werden muss, dass die Schrittzahl möglichst gering ist. Dabei ist der Parameter k für alle n Scheiben im Allgemeinen ein anderer Wert als der Wert für k, der im ersten und dritten Schritt genau k Scheiben verschiebt.
Wählen Sie links oben 4 Stangen aus, so können Sie diese Variante untersuchen. Auch hier können Sie mit Mausklick Scheiben verschieben und so selbst nach einer optimalen Zugfolge suchen.
| Turm von Hanoi |
|---|
 |
| Herunterladen |
Hinweis: Dieses Programm enthält einen speziellen Algorithmus und ermittelt so eine optimale Abfolge der Scheibenbewegungen!
Die kürzeste Zugfolge für maximal 72 Scheiben wird im Lexikon des Programms auf der Seite Vierstangen-Turm von Hanoi (2) berechnet.
Download
Ein Einzelprogramm, das nur die Aufgabe für 3- und 4-Stangen-Türme von Hanoi enthält, ist ladbar.
Dreifarben-Turm von Hanoi
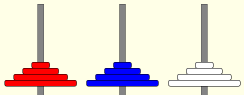 Eine weitere, interessante Variante des Spiels ist der mehrfarbige Turm von Hanoi.
Eine weitere, interessante Variante des Spiels ist der mehrfarbige Turm von Hanoi.
In diesem Fall befinden sich auf allen 3 Stangen die gleichen Scheiben, jedoch unterschiedlich gefärbt. Ziel ist es, die farbigen Türme um eine Position weiterzuverschieben oder die Lage von zwei Türmen auszutauschen. Dabei dürfen wieder nur Scheiben auf größere oder gleich große gelegt werden.
Überraschend ist auch dieses Problem lösbar.
Für n = 3, 4, 5, … Scheiben auf jeder Stange benötigt man im optimalen Fall eine Zugzahl von 80, 192, 424, 896, 1848, 3760, 7592, 15264, 30616, 61328, …
Der Tauschalgorithmus ist anspruchsvoll und besteht aus mehreren rekursiven Aufrufen des Tauschverfahrens des ursprünglichen Spiels.
Dieses Teilprogramm demonstriert auch einen Dreifarben-Turm von Hanoi.
Beachten Sie bitte, dass die Berechnungszeit der Züge ab 9 Scheiben hoch ist und mit höherer Scheibenzahl schnell stark ansteigt.