 Gegeben ist ein Rechteck-Gitter der Größe a x b.
Gegeben ist ein Rechteck-Gitter der Größe a x b.
Gesucht ist die Anzahl aller möglichen Wege vom Anfang, dem Punkt (0,0), zum Ziel nach (a,b), wenn ausschließlich Schritte (1,0), (0,1) und (1,1) möglich sind.
Durch Delannoy wurde eine mathematische Lösung gefunden.
Die Delannoy-Zahlen werden definiert durch:
D(a,b) = D(a-1,b) + D(a,b-1) + D(a-1,b-1)
wobei D(0,0) = 1 ist.
Diese Zahlen geben die Anzahl der gesuchten Wege vom Punkt (0,0) zum Punkt (a,b) an. Gilt n = a = b, so ergeben die Delannoy-Zahlen die Anzahl der direkten Königszüge im Schach.
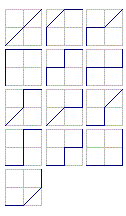 In der Abbildung sind die 13 möglichen Wege für ein 2 x 2 Feld eingezeichnet.
In der Abbildung sind die 13 möglichen Wege für ein 2 x 2 Feld eingezeichnet.
Für die ersten Delannoy-Zahlen D(n,n) ergibt sich für n = 0,1,2,3,…: 1, 3, 13, 63, 321, 1683, 8989, 48639, 265729, 1462563, 8097453, 45046719, 251595969, 1409933619, 7923848253, 44642381823, 252055236609, 1425834724419, 8079317057869, 45849429914943, 260543813797441, …
Eng verbunden mit den Delannoy-Zahlen sind die Schröder-Zahlen.
Die Schröder-Zahl S(n) ist die Anzahl der möglichen Wege auf einem Gitter vom Punkt (0,0) zum Punkt (n,n), wenn nur Schritte (0,1), (1,0) und (1,1) zugelassen sind und die Gerade y = x nie überschritten werden darf. Damit beschränken sich die Wege auf ein Dreiecksgitter. Für diese Wege wurde durch Schröder eine mathematische Lösung gegeben:
S(n) = S(n-1) + Σ k=0 n-1 (S(k) S(n-1-k)) ; S(0)=1
Die ersten Schröder-Zahlen S(n) sind 2, 6, 22, 90, 394, 1806, 8558, 41586, 206098, 1037718, 5293446, 27297738, 142078746, 745387038, 3937603038, 20927156706, 111818026018, 600318853926, 3236724317174, 17518619320890, 95149655201962, 518431875418926, 2832923350929742, 15521467648875090, 85249942588971314, …
Das Problem der Wegsuche kann durch Sperren von einzelnen Weggabelungen erweitert werden. Ebenso ist es möglich, die Schröder-Zahlen auch auf rechtwinklige Dreiecke zu erweitern, deren Katheten nicht gleich lang sind.
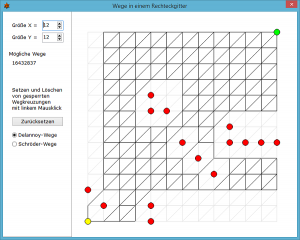
In diesem Programmteil kann die Größe des Rechteckgitters bis maximal 25 in jeder Richtung eingestellt werden. Weggabelungen können durch linken Mausklick auf einen Gitterpunkt gesetzt oder gelöscht werden. Je nach gesperrter Weggabelung werden die nicht erreichbaren Punkte besonders gezeichnet.
Ebenso kann man zwischen Delannoy-Wegen und Schröder-Wegen wählen.
| Wege im Rechteckgitter | |
|---|---|
 |
|
| Herunterladen | |
Download
Download des Einzelprogramms: