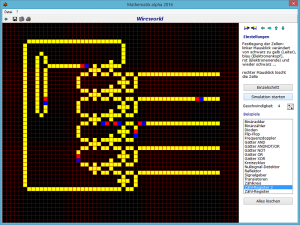
 Wireworld ist ein zellulärer Automat, der erstmals von Brian Silverman 1987 entwickelt wurde. Wireworld eignet sich besonders für die Simulation elektronischer Logikelemente wie Gatter oder Flip-Flops. Trotz der Einfachheit seiner Regeln ist es möglich, vollständige Computer mittels Wireworld zu implementieren.
Wireworld ist ein zellulärer Automat, der erstmals von Brian Silverman 1987 entwickelt wurde. Wireworld eignet sich besonders für die Simulation elektronischer Logikelemente wie Gatter oder Flip-Flops. Trotz der Einfachheit seiner Regeln ist es möglich, vollständige Computer mittels Wireworld zu implementieren.
Eine Wireworld-Zelle kann vier unterschiedliche Zustände einnehmen (die jeweils angegebene Farbe wird in den animierten Grafiken auf dieser Seite verwendet):
- leer (schwarz)
- „elektrischer Leiter“ (gelb)
- „Elektronenkopf“ (blau)
- „Elektronenende“ (rot)
Die Zeit verläuft in diskreten Schritten, den sogenannten Generationen. Dabei bleibt eine leere Zelle grundsätzlich leer. Die übrigen Zellen verhalten sich beim Übergang von einer Generation zur nächsten wie folgt:
- Aus einem Elektronenkopf wird ein Elektronenende.
- Aus einem Elektronenende wird ein Leiter.
- Aus einem Leiter wird ein Elektronenkopf, wenn genau ein oder zwei der benachbarten Zellen Elektronenköpfe sind.
Durch die geeignete Ausbildung von Leiterverzweigungen und -kreuzungen können logische Schaltelemente vom einfachen Gatter bis zum komplexen Rechenwerk realisiert werden.
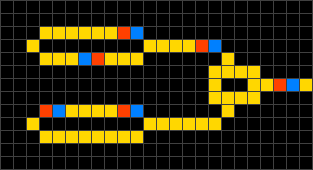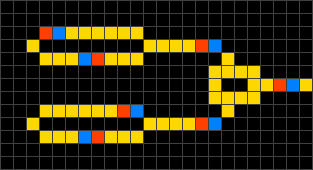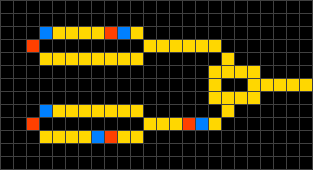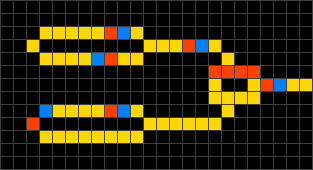 Dieser Zellularautomat kann in diesem Teilprogramm getestet werden.
Dieser Zellularautomat kann in diesem Teilprogramm getestet werden.
Dazu geben Sie zuerst mit der Maus eine Ausgangssituation ein. Ein linker Mausklick verändert eine Zelle zyklisch von Schwarz nach Blau, Rot, Gelb und wieder Schwarz, ein rechter Mausklick löscht die Zelle.
Die Ausgangssituationen können Sie über die zwei kleinen Schalter auf der Festplatte speichern bzw. wieder laden.
Zum Starten der Simulation klicken Sie auf den entsprechenden Schalter. An den kleinen Pfeilschaltern ist die Geschwindigkeit einstellbar.
| Zellularautomat Wireworld | |
|---|---|
 |
|
| Herunterladen | |
Download
Dieser Programmteil steht als Einzelprogramm zum Download zur Verfügung.