 Ein im 16.-17. Jahrhundert sehr beliebtes Problem der Mathematik war die Frage nach der Form von Kurven, die entstehen, wenn ein Kreis auf einer anderen Kurve abrollt.
Ein im 16.-17. Jahrhundert sehr beliebtes Problem der Mathematik war die Frage nach der Form von Kurven, die entstehen, wenn ein Kreis auf einer anderen Kurve abrollt.
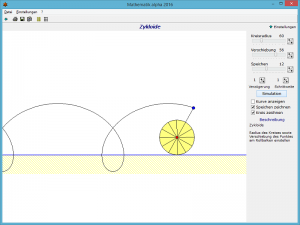
Rollt ein Kreis auf einer Geraden ab, so entsteht eine sogenannte Zykloide. Auch hier können Sie Parameter verändern.
Über den Rollbalken Kreisradius stellen Sie die Größe des rollenden Kreises ein, mit Verschiebung den Abstand des Kurven erzeugenden Punktes vom Mittelpunkt des Kreises. In der Abbildung rollt ein Kreis mit dem Radius 30 bei einer Verschiebung von 25 auf der Geraden ab. Markieren Sie das Feld Kurve anzeigen, so wird die entstehende Gesamtkurve dargestellt.
 Wählen Sie nun Simulation, beginnt das Programm den Kreis abrollen zu lassen und konstruiert so die gewählte Zykloide.
Wählen Sie nun Simulation, beginnt das Programm den Kreis abrollen zu lassen und konstruiert so die gewählte Zykloide.
Zykloiden wurden intensiv 1599 von Galilei untersucht. Dabei versuchte er mittels Metallstücken in Form von Zykloiden die Flächeninhalte unter Kurven zu bestimmen.
Für eine positive Verschiebung entsteht eine verlängerte Zykloide, für negative Verschiebungen eine verkürzte Zykloide. Beide werden auch Trochoide genannt.
Erste Studien der Zykloide gehen auf Charles Bouvelles 1501 zurück, der auch den Namen (griechisch „κυκλος“ = „Kreis“) prägte. Den Wert der Fläche unter der Kurve (3πa²) gaben Torricelli und später Fermat und Descartes an. Roberval (1634) und Wren (1658) ermittelten die Länge eines Zykloidenbogens zu 8a.
1692 zeigte Jakob Bernoulli, dass die Zykloide die Katakaustik eines Kreises ausgehend von einem Punkt auf der Kreisperipherie ist. 1696 wies Johann Bernoulli nach, dass die Zykloide das Brachistochron-Problem löst.
Beim Brachistochronen-Problem wird gefragt, auf welcher Bahnkurve sich ein Massenpunkt reibungsfrei von einem oberen zu einem unteren Punkt in kürzester Zeit bewegen kann. Der Name der Kurve ergibt sich aus dem griechischen „brakhisto“ = „am kürzesten“ und „chronos“ = „Zeit“. Erstaunlicherweise kann sich der Punkt auf einer Kurve bewegen, die sogar unterhalb des Zielpunktes verläuft, einer Zykloiden.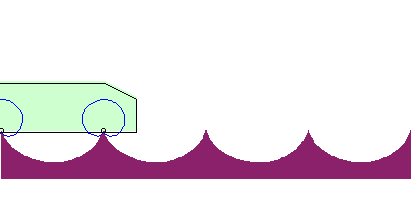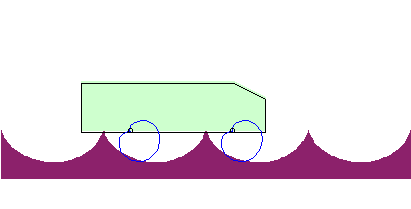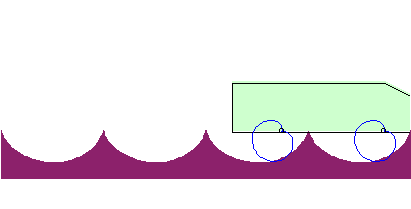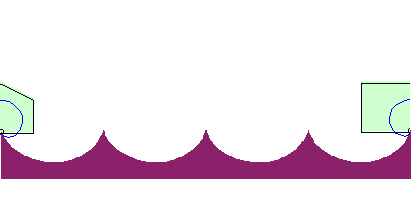 Ein Fahrzeug könnte sich auf einer Straße in Zykloidenform völlig waagerecht bewegen. Allerdings müssten die Räder dann Kardioiden sein.
Ein Fahrzeug könnte sich auf einer Straße in Zykloidenform völlig waagerecht bewegen. Allerdings müssten die Räder dann Kardioiden sein.
Epi- und Hypozykloide
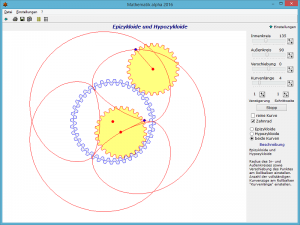 Ein im 16.-17. Jahrhundert sehr beliebtes Problem der Mathematik war die Frage nach der Form von Kurven, die entstehen, wenn ein Kreis auf einer anderen Kurve abrollt. Insbesondere das Rollen innerhalb oder außerhalb eines anderen Kreises faszinierte Mathematiker wie Dürer, Galilei, Desargues, Huygens, Fermat, Descartes, die Bernoullis, Leibniz, Newton, l’Hospital, Euler usw. – also nahezu alle führenden Personen der Mathematik dieses Zeitalters.
Ein im 16.-17. Jahrhundert sehr beliebtes Problem der Mathematik war die Frage nach der Form von Kurven, die entstehen, wenn ein Kreis auf einer anderen Kurve abrollt. Insbesondere das Rollen innerhalb oder außerhalb eines anderen Kreises faszinierte Mathematiker wie Dürer, Galilei, Desargues, Huygens, Fermat, Descartes, die Bernoullis, Leibniz, Newton, l’Hospital, Euler usw. – also nahezu alle führenden Personen der Mathematik dieses Zeitalters.
Rollt der Kreis außerhalb eines anderen und markiert man auf der Kreisperipherie einen Punkt, spricht man von einer entstehenden Epizykloide als Rollkurve. Bewegt sich der Kreis innerhalb eines zweiten Kreises liegt eine Hypozykloide vor. Je nach Größenverhältnis beider Kreise zueinander entstehen unterschiedlichste Kurvenbilder.
Dieses Teilprogramm gibt Ihnen die Möglichkeit, derartige Kurven zu konstruieren.
 In diesem Teilprogramm stellen Sie an den Rollbalken
In diesem Teilprogramm stellen Sie an den Rollbalken
Folgendes ein:
- Innenkreis … den Radius des inneren Kreises, d.h. des Kreises, auf dem der zweite rollt
- Außenkreis … den Radius des rollenden Kreises
- Verschiebung … die Größe, um die der zeichnende Punkt auf dem rollenden Kreis nach außen (positiver Wert) oder nach innen (negativer Wert) verschoben wird
- Kurvenlänge … die Anzahl der vollen Umläufe, die maximal gezeichnet werden. Insbesondere für Innenkreis- und Außenkreisradien, die nicht in einem kleinen Verhältnis, z.B. 1:2 oder 3:4, stehen, kann so eine aussagekräftigere Kurve erzeugt werden.
Ob Sie eine Epizykloide, eine Hypozykloide oder gleichzeitig beide zeichnen wollen, stellen Sie an den Auswahlfeldern ein.
Wählen Sie nun Simulation, beginnt das Programm den Kreis abrollen zu lassen und konstruiert so die gewählte Zykloide. Die Geschwindigkeit stellen Sie an dem Rollbalken neben dem Simulation-Schalter ein. Um die Simulation zu stoppen, drücken Sie den Schalter noch mal.
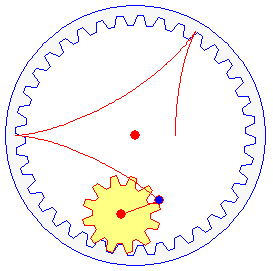 Eine besondere Darstellung erhalten Sie, wenn Sie das Markierungsfeld Zahnrad auswählen. In diesem Fall stellt das Programm auf- und ineinander rollende Zahnräder dar, die die gleichen Rollkurven erzeugen.
Eine besondere Darstellung erhalten Sie, wenn Sie das Markierungsfeld Zahnrad auswählen. In diesem Fall stellt das Programm auf- und ineinander rollende Zahnräder dar, die die gleichen Rollkurven erzeugen.
Interessante Kurven ergeben sich z.B. für
- Hypozykloide mit Innenkreis 100, Außenkreis 50 … senkrechte Gerade
- Hypozykloide mit Innenkreis 200, Außenkreis 50 … Astroide
- Hypozykloide mit Innenkreis 100, Außenkreis 50, Verschiebung -50 … Kreis mit Radius 50
- Hypozykloide mit Innenkreis 100, Außenkreis 25, Verschiebung -15 … „Quadrat“ mit abgerundeten Ecken
- Hypozykloide mit Innenkreis 100, Außenkreis 25, Verschiebung +50 … „Vierblättriges Kleeblatt“
- Epizykloide mit Innenkreis 60, Außenkreis 60, Verschiebung 0 … Kardioide
| Epi- und Hypozykloide | |
|---|---|
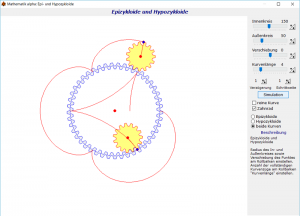 |
|
| Herunterladen | |
Markieren Sie das Feld reine Kurve, werden die erzeugenden Kreise nicht dargestellt. Das Programm zeigt in diesem Fall nur die entstehende mathematische Kurve.
Dieser Programmteil ist auch als Einzelprogramm verfügbar.
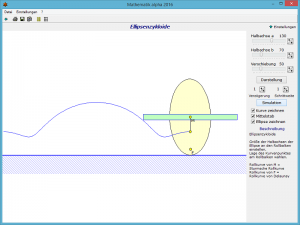
Ellipsenzykloide
 Rollt ein Kreis auf einer Geraden ab, so beschreibt ein Punkt auf der Kreisperipherie eine Zykloide. Auch andere Kurven, außer dem Kreis, können auf einer Geraden abrollen. Erstmals wurde dies 1869 durch Besant untersucht.
Rollt ein Kreis auf einer Geraden ab, so beschreibt ein Punkt auf der Kreisperipherie eine Zykloide. Auch andere Kurven, außer dem Kreis, können auf einer Geraden abrollen. Erstmals wurde dies 1869 durch Besant untersucht.
Zum Beispiel beschreibt der Brennpunkt einer Ellipse während des Abrollens eine Rollkurve nach Delaunay.
Beschreibt ρ0 = f(θ0) die abrollende Kurve, so ergibt sich die allgemeine Rollkurve zu
x = ∫ (f(t) f'(t)) · dy/dt · dt ; y = f(t) / √(f(t)² +f'(t)²))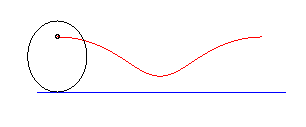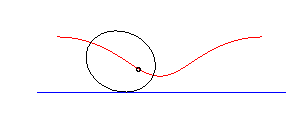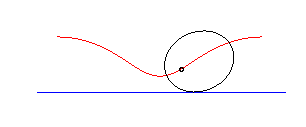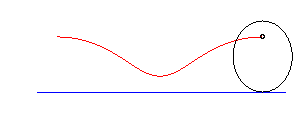
In diesem Teilprogramm kann eine Ellipse längs einer Geraden abrollen.
An den Rollbalken stellen Sie die Größe der Halbachsen der Ellipse ein. Klicken Sie nun auf Simulation, so rollt die Ellipse derart ab, dass der Winkel im Mittelpunkt der Ellipse kontinuierlich erhöht wird. Interessant ist dabei, dass die Ellipse am „spitzen“ Ende eine größere Winkelgeschwindigkeit aufweist als am „flachen“.
| Ellipsenzykloide |
|---|
 |
| Herunterladen |
Innerhalb der Ellipse können Sie die Lage eines Punktes mit Verschiebung verändern. Für diesen Punkt wird die Rollkurve gezeichnet. Liegt der Punkt nicht auf der Ellipse, so ergibt sich eine verlängerte oder verkürzte elliptische Zykloide, eine elliptische Trochoide.
Die Ellipsenzykloide wird zu einer klassischen Standardzykloide, wenn die Ellipse ein Kreis ist und ein Punkt auf der Kreisperipherie betrachtet wird.
Die Ellipsenzykloide ist auch als Einzelprogramm ladbar.
Polygonzykloide
 Rollt ein Kreis auf einer Geraden ab, so beschreibt ein Punkt auf der Kreisperipherie eine Zykloide. Auch andere geometrische Figuren, außer dem Kreis, können auf einer Geraden abrollen.
Rollt ein Kreis auf einer Geraden ab, so beschreibt ein Punkt auf der Kreisperipherie eine Zykloide. Auch andere geometrische Figuren, außer dem Kreis, können auf einer Geraden abrollen.
Zum Beispiel beschreibt der Brennpunkt einer Ellipse während des Abrollens eine Rollkurve nach Delaunay.
Rollt ein regelmäßiges Polygon ab, so entsteht eine Kurve, die sich aus mehreren Teilstücken in Form von Zykloiden zusammensetzt.
In diesem Teilprogramm können regelmäßige Polygone längs einer Geraden abrollen.
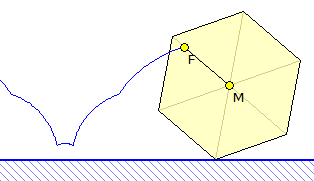 An den Rollbalken stellen Sie die Größe des Polygons und dessen Eckenzahl ein.
An den Rollbalken stellen Sie die Größe des Polygons und dessen Eckenzahl ein.
Klicken Sie nun auf Simulation, so rollt das Vieleck derart ab, dass der Winkel im Mittelpunkt des Polygons kontinuierlich erhöht wird, d.h. das Vieleck kippt jeweils über die rechte untere Ecke.
| Polygonzykloide |
|---|
 |
| Herunterladen |
Innerhalb des Polygons können Sie die Lage eines Punktes mit Verschiebung verändern. Für diesen Punkt wird die Rollkurve gezeichnet. Der Schalter Darstellung setzt das Vieleck auf den Anfang zurück.
Download
Das Teilprogramm Polygonzykloide ist auch als Einzelprogramm ladbar.
Anmerkung:
Da mehrfache angefragt wurde, ob dem Autor eine geschlossene Gleichung für die Ellipsoidenzykloide bekannt ist, wird folgendes erklärt:
Eine einzelne Formel bzw. eine Abfolge von Formeln ist nicht bekannt. Im Programm wird eine Näherungslösung berechnet:
1. Für einen jeweils kleinen Winkel wird die Bogenlänge der Ellipse berechnet, was nur näherungsweise möglich ist, da es keine „einfache“ Gleichung für die Bogenlänge einer Ellipse gibt. Es ist ein elliptisches Integral, d.h. nicht auflösbar. Damit ist schon klar, dass es keine einzelne Formel geben kann.
2. Danach wird die Lage der Tangente an die Ellipse für diesen Winkel ermittelt und die ganze Ellipse um den Winkel zwischen Tangente und Untergrund bzgl. des Berührungspunktes auf dem Untergrund gekippt.
3. In der grafischen Darstellung wird die Ellipse punktweise für die gedrehte Lage gezeichnet. Dazu muss der Mittelpunkt der Ellipse bei der Drehung ermittelt werden.
4. Der Punkt, welcher die Zykloide beschreibt, wird dann aus dem neuen Mittelpunkt und dem Endpunkt der Halbachse berechnet.
Insgesamt ist diese keinen Fall einfache Mathematik.
Unter https://math.stackexchange.com/questions/1803005/parametric-equation-of-elliptical-cycloidal-sine-curve wurde vor Jahren schon nach einer Lösung gefragt; ohne Ergebnis.
Unter https://www.programmersought.com/article/18253960726/ gibt es eine Lösung in Mathematica.