 Von Michael Barnsley wurde folgendes Chaosspiel erfunden:
Von Michael Barnsley wurde folgendes Chaosspiel erfunden:
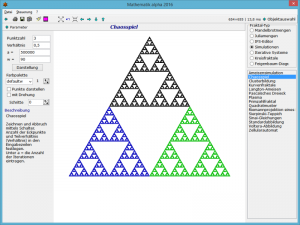
Gegeben sind drei Punkte A, B und C eines gleichseitigen Dreiecks und zusätzlich ein beliebiger Punkt P1 der Zeichenebene. Als Nächstes wird ein beliebiger Eckpunkt des Dreiecks gewählt, z.B. C. Nun bildet man den Mittelpunkt P2 der Strecke von P1 nach C und markiert diesen. Erneut wird ein Dreieckspunkt, z.B. A gewählt und der Mittelpunkt P3 von P2 nach A gebildet und markiert usw. Ergebnis: das berühmte Sierpinski-Dreieck.
Der Mathematiker Sierpinski hat das Sierpinski-Dreieck 1910 zu dem Zweck in die mathematische Welt gesetzt, dass seine Studenten begreifen, dass sie Begriffe Linie und Fläche durchaus nicht trivial sind.
Wenn man aus einem Dreieck die Mitte herausnimmt und aus den drei Restdreiecken wieder die Mitte, und wieder und wieder…, ist es dann eigentlich noch eine Fläche?
Nein! Die Dimension ist nicht 2 noch 1, sondern ln(3)/ln(2)=1,58…; es ist ein Fraktal. (fractum, lat.= gebrochen)
Interessant ist, dass dieses Chaosspiel auch für vier, fünf oder noch mehr Ausgangspunkte verblüffende Ergebnisse liefert. Dabei ist allerdings zu beachten, dass nun nicht mehr die Strecke halbiert, sondern ein gewisser Abstand von den gefundenen Punkten P(i) gewählt wird. Für fünf Punkte beträgt er z.B. 62,4% der Gesamtstrecke, für sechs Punkte 66,67%. Verallgemeinert man dies auf n Ausgangspunkte, so ergibt sich ein guter Näherungswert zu n / (n + 3).
Dieses Teilprogramm ermöglicht Ihnen die Simulation des Chaosspiels. Geben Sie unter Punktzahl die Zahl der Ausgangspunkte und unter Codierung den Faktor zur Ermittlung des jeweils neuen Punktes an, also für drei Punkte z.B. 0,5. Allerdings ist auch jeder andere Wert größer als 0 und kleiner als 1 möglich. Tragen Sie einen Wert gleich 0 ein, ermittelt das Programm automatisch den für die Punktzahl günstigsten Wert der Codierung.
Betätigen Sie nun den Schalter Darstellung, zeichnet das Programm genau 500000 Punkte des Chaosspiels. Markieren Sie das Feld Punkte darstellen, so zeichnet das Programm die Ausgangspunkte.
Wird das Feld Drehung gewählt, so dreht der Algorithmus vor dem Zeichnen der Punkte diese stets um den Zielpunkt mit dem eingegeben Winkel w (in °). Dabei entstehen weitere merkwürdige Gebilde.
Möchten Sie die Konstruktion schrittweise verfolgen, so können Sie an den zwei Schaltern an der unteren Skala Schritte jeweils einen Punkt mehr bzw. auch weniger zeichnen. Angezeigt werden die Zielpunkte, die schon gezeichneten Punkte und besonders hervorgehoben werden der letzte Punkt P und die Strecke, die zu seinem Erreichen halbiert wurde. Maximal können Sie in diesem Schrittmodus 2500 Punkte darstellen.
Download
Eine sehr einfache Umsetzung dieses Programmteils kann hier als Einzelprogramm heruntergeladen werden. Das Programm ist ein einfaches Übungsprogramm für die Informatikausbildung von Schülern der Klassenstufe 9/10 und entspricht nicht dem Niveau des Programmteils in „Mathematik alpha“.
| Chaosspiel (Exe + Quelltext) | Herunterladen |