Mathematische Kurven werden mitunter nicht in Parameterform oder Polarkoordinatenform definiert. Unter Umständen ist eine einfache Gleichung auch nur in impliziter Form möglich, zum Beispiel bei der Doppelhorn-Kurve
0 = y² (p² – x²) – (x² + 2py – p)²
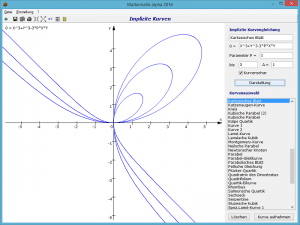Derartige implizite Darstellungen können Sie in diesem Teilprogramm untersuchen.
Tragen Sie dazu unter 0 = den impliziten Term ein oder wählen Sie eine der vordefinierten Kurven aus. Nach einem Klick auf den Schalter Darstellung wertet das Programm die Gleichung aus.
Dabei werden Punkte in der Darstellungsebene gesucht, die der Gleichung möglichst gut entsprechen. Die Darstellung erfolgt in zwei Schritten: Zum einen werden die Punkte mit abnehmender Ordinate gesucht, zum Zweiten die mit zunehmender Abszisse. Dadurch erfordert das Zeichnen der Kurve auch eine gewisse Zeit.
Weitere Eingabemöglichkeiten, Parameter P (Anfangswert), bis = (Endwert) und Δ = (Schrittweite), können zur Darstellung von Kurvenscharen verwendet werden.
Die Bibliothek der vordefinierten Kurven können Sie erweitern. Tragen Sie dazu eine Kurvengleichung und in der Eingabezeile darüber einen Kurvennamen ein. Mit dem Schalter Kurve aufnehmen wird Ihre Eingabe eingefügt.
Eine markierte Kurve der Tabelle können Sie mit dem Schalter Löschen aus der List entfernen.
| Implizite Kurven |
|---|
|
| Herunterladen |
Download
Dieses Teilprogramm steht in vereinfachter Form als eigenständiges Programm zum Download bereit.