Palindrom-Zahlen sind Zahlen, deren Wert sich nicht ändert, wenn sie von hinten nach vorn gelesen werden.
Der Begriff Palindrom kommt aus dem Griechischen und bedeutet „Hin- und Herbewegung“ (παλινδρομηση = palíndromese).
Die ersten Palindrom-Zahlen sind außer den einstelligen 11, 22, 33, 44, 55, 66, 77, 88, 99, 101, 111, 121, 131, …
Die Anzahl der Palindrome unter 10, 10², 10³, … ergibt sich zu 9, 18, 108, 198, 1098, 1998, … und allgemein 9 · 10^((n-1)/2) für ungerades n, 9 · 10^(n/2 -1) für gerades n.
Die Summe der Reziproken aller Palindrome konvergiert. Eine Computerberechung aller 1999999998 Palindromreziproken bis 18 Ziffern ergab die Näherungssumme 3,37028325668…
Zur Berechnung der n.ten Palindromzahl existiert eine Formel:
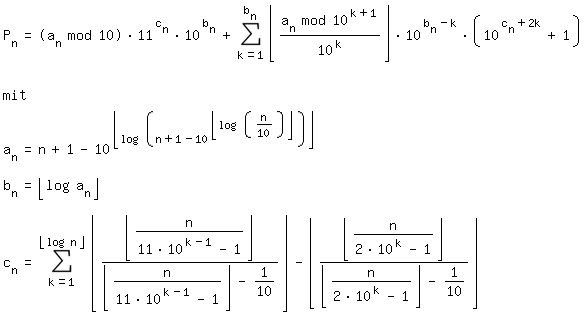
Palindrom-Primzahlen, Umkehrbare Primzahlen
Palindrom-Primzahlen, auch umkehrbare Primzahlen genannt, sind Primzahlen, deren Wert sich nicht ändert, wenn sie von hinten nach vorn gelesen werden.
Die ersten derartigen Zahlen sind 2, 3, 5, 7, 11, 101, 131, 151, 181, 191, …
Die Anzahl der palindromischen Primzahlen mit 1, 2, 3, … Ziffern ist 4, 1, 15, 0, 93, 0, 668, 0, 5172, 0, 42042, 0, …
Die Anzahl der Palindrom-Primzahlen unter 101, 102, 103, … wird 4, 5, 20, 20, 113, 113, 781, 781, 5953, 5953, 47995, 47995, …
Da jede Palindrom-Zahl mit einer geraden Anzahl von Ziffern durch 11 teilbar ist, existiert nur eine Palindrom-Primzahl mit gerader Stellenzahl, die 11.
2001 fand Harvey Dubner die bisher größte Palindrom-Primzahl mit 39027 Ziffern:
P = 1039026 + 4538354 · 1019510 + 1.
 Durch G.L.Honaker wurde auch eine Pyramide angegeben, die nur aus Palindrom-Primzahlen besteht.
Durch G.L.Honaker wurde auch eine Pyramide angegeben, die nur aus Palindrom-Primzahlen besteht.
Palindromzahlen mit Palindrom-Dreieckszahlen
Eine Dreieckszahl D ist von der Struktur n(n+1)/2.
Palindromzahlen n, deren Dreieckszahl ebenfalls Palindrom ist, sind selten.
Durch Hans-Jürgen Caspar wurden 8 derartige Zahlen angegeben. Weitere konnten durch massiven Computereinsatz ermittelt werden (Stand 25. April 2016, gesucht bis 61270011007216):
| Palindrom | Palindrom-Dreieckszahl |
| 11 | 66 |
| 77 | 3003 |
| 363 | 66066 |
| 1111 | 617716 |
| 2662 | 3 544453 |
| 111111 | 6172 882716 |
| 246642 | 30416 261403 |
| 11111111 | 61 728399 382716 |
| 363474363 | 66056 806460 865066 |
| 2664444662 | 3 549632 679762 369453 |
| 26644444662 | 354 963215 686512 369453 |
| 246644446642 | 30416 741529 792514 761403 |
| 266444444662 | 35496 321045 754012 369453 |
| 2466444446642 | 3 041674 104186 814014 761403 |
Palindrom-Zahlen und der 196-Algorithmus
Gegeben ist eine zwei- oder mehrstellige natürliche Zahl n.
Zu dieser Zahl wird die natürliche Zahl addiert, welche dadurch entsteht, dass die Ziffernfolge von n umgekehrt wird. Diese Addition wird mit der Summe immer wiederholt, bis eine Palindrom-Zahl entsteht.
z.B. n = 5180 5280, 6105, 11121, 23232
Die entstehende Zahl kann teilweise sehr groß werden, z.B. für 89 ergibt sich 8813200023188.
Die kleinsten Zahlen, für welche nicht bekannt ist, ob der Algorithmus irgendwann eine Palindrom-Zahl liefert, sind:
196, 887, 1675, 7436, 13783, …
Diese Zahlen werden auch Lychrel-Zahlen genannt.
1990 ermittelte John Walker 2415836 Iterationen für n=196. Im Jahre 1995 erweiterte Tim Irvin die Suche bis zu ersten auftretenden Zahl mit 2 Millionen Ziffern. Nach 9,48 Millionen Iterationen ergab sich später eine nichtpalindrome Zahl mit 3924257 Ziffern.
Bis zum 1.Mai 2006 berechnete Wade VanLandingham fünf Jahre 724756966 Iterationen der 196. Die letzte Ergebniszahl hatte 300 Millionen Stellen und war immer noch kein Palindrom.
Bis zu einem Zwischenergebnis von 1000stelligen Zahlen findet man für folgende Werte < 1000 kein Palindrom:
196, 295, 394, 493, 592, 689, 691, 788, 790, 879, 887, 978, 986
Die Anzahl a(n) der bis zum Erreichen der Palindrom-Zahl nötigen Iterationen sind für n=1, 2, …
1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 2, 2, 2, 2, 2, 2, 3, 2, 2, 1, …
Die kleinste Zahl, welche a(n) = 0,1,2,3,… benötigt, ist
0, 10, 19, 59, 69, 166, 79, 188, 193, 1397, 829, 167, 2069, 1797, 849, 177, 1496, 739, 1798, 10777, 6999, 1297, 869, 187, 89, 10797, 10853, 10921, 10971, 13297, 10548, 13293, 17793, 20889, ?, ?, ?, 80359, 13697, 10794, 15891, …
Unter den ersten 100000 Zahlen fand man 5996 Zahlen, die bisher keine Palindrome ergaben.
Durch Jason Doucette wird eine kontinuierliche Suche nach Lösungen des 196-Algorithmus durchgeführt. Dabei fand er immer wieder neue Rekord-Palindromzahlen und höhere Werte für die notwendigen Iterationen bis zum Erreichen des Palindroms.
| Zahl | Iterationen | entstehendes Palindrom |
| 79 | 6 | 44044 |
| 89 | 24 | 8 813200 023188 |
| 6999 | 20 | 16 668488 486661 |
| 10548 | 30 | 17858 768886 785871 |
| 10677 | 53 | 4668 731596 684224 866951 378664 |
| 147996 | 58 | 8 834453 324841 674761 484233 544388 |
| 150296 | 64 | 682 049569 465550 121055 564965 940286 |
| 1000689 | 78 | 796 589884 324966 945646 549669 423488 985697 |
| 1005744 | 79 | 796 589884 324966 945646 549669 423488 985697 |
| 1017501 | 80 | 14 674443 960143 265333 356234 106934 447641 |
| 7008899 | 82 | 68 586378 655656 964999 946965 655687 368586 |
Der aktuelle Rekord liegt bei 261 Iterationsschritten. Dies benötigt die Zahl 1186060307891929990 (19 Stellen), um auf ein 119-stelliges Palindrom zu kommen.
| 196-Algorithmus | |
|---|---|
| Herunterladen |
Download
Für die Untersuchung des 196-Algorithmus enthält „Mathematik alpha“ ein Teilprogramm.
Der 196-Algorithmus kann aber auch als eigenständiges Programm geladen werden.