Die Pellsche Gleichung
X² – D Y² = 1
ist eine Diophantische Gleichung 2.Ordnung und erhielt ihren Namen von Euler zu Ehren von John Pell (1611-1685).
Für D = 61 und 109 ist die Lösung extrem schwierig und wurde erstmals von Lord William Brouncker und John Wallis gefunden. Z.B. ergibt sich für D = 109:
X = 158070671986249 ; Y = 15140424455100
Kennt man eine Lösung x0 und y0, so ergeben sich weitere Lösungen mit
x1 = C x0 -1 ; y1 = C y0 mit C = 2 x0
xn = C xn-1 – xn-2 ; yn = C yn-1 – yn-2
Die Liste enthält die kleinsten Lösungen der Pellschen Gleichung für die ersten quadratfreien D:
| D | Lösungen | D | Lösungen |
| 5 | 9 ; 4 | 6 | 5; 2 |
| 7 | 8 ; 3 | 10 | 19; 6 |
| 11 | 10 ; 3 | 13 | 649 ; 180 |
| 14 | 15 ; 4 | 15 | 4 ; 1 |
| 17 | 33 ; 8 | 19 | 170 ; 39 |
| 21 | 55 ; 12 | 22 | 197 ; 42 |
Die Lösung der Pellschen Gleichung X² – D·Y² = 1 ergibt schon für kleine D sehr große Lösungen X und Y. Die Tabelle enthält die Werte für D, bei denen X ein neues Maximum annimmt.
| D | Wert für X |
| 5 | 9 |
| 10 | 19 |
| 13 | 649 |
| 29 | 9801 |
| 46 | 24335 |
| 53 | 66249 |
| 61 | 1766 319049 |
| 109 | 158 070671 986249 |
| 181 | 2 469645 423824 185801 |
| 277 | 159 150073 798980 475849 |
| 397 | 838 721786 045180 184649 |
| 409 | 25052 977273 092427 986049 |
| 421 | 3879 474045 914926 879468 217167 061449 |
| 541 | 370745 336002 386702 880064 559966 700500 |
| 661 | 16 421658 242965 910275 055840 472270 471049 |
| 1021 | 198723 867690 977573 219668 252231 077415 636351 801801 |
| 1069 | 742925 865816 843150 858935 268959 512942 700219 559049 |
Die Schlacht von Hastings
aus „Amusements in Mathematics“, von Henry Ernest Dudeney, 1917
Die Aufgabe bezieht sich auf die Schlacht bei Hastings, jenen berühmten Kampf, in dem 1066 die Normannen unter Wilhelm dem Eroberer die Sachsen unter König Harald besiegten, und fortan die Geschicke Englands bestimmten. Nach Dudeney schildert die alte Chronik:
„Haralds Mannen standen tapfer zusammen und bildeten 61 Quadrate mit gleich vielen Recken in jedem Quadrat. Als Harald sich in die Schlacht warf, bildeten die Sachsen mit ihm zusammen ein einziges, mächtiges Quadrat.“
Gesucht ist nun die minimal mögliche Anzahl der Krieger.
Lösung: Wir bezeichnen die Kantenlänge der kleinen Quadrate mit y und die vom großen Quadrat mit x, d.h.
61 y² + 1 = x²
Die kleinste natürliche Lösung dieser Pellschen Gleichung ist y = 226153980, x = 1766319049.
Mit Harald zusammen wäre also etwa 3,11 Trillionen Sachsen dabei gewesen. Und da sollen die verloren haben?
Pellsche Gleichung und Quadratwurzel
Mittels Pellscher Gleichung X² – D·Y² = 1 kann eine Näherungsformel für die Quadratwurzel √D ermittelt werden.
Durch Umstellen ergibt sich mit der Lösung (x0, y0) als 1.Näherung
√D ≈ x0 / y0
Mit der Lösung (xn, yn) ist auch
xn+1 =xn² + D yn² ; yn+1 = 2 xn yn
Lösung der Gleichung, wobei die Quotienten xn / yn mit wachsendem n immer besser die Wurzel √D annähern.
Eine schnellere Konvergenz ergibt sich durch Abschätzen des Fehlers
√D = x0/y0 – 1/2 (1/(x0 y0) + 1/(x1 y1) + 1/(x2 y2) + …)
Zum Beispiel wird für D = 2: x0 = 3, y0 = 2, x1 = 9+2·4 = 17, y1 = 2·3·2 = 12, x2 = 289+2·144 = 577, y2 = 2·17·12 = 408 und somit
√2 = 3/2 – 1/2 (1/(3·2) + 1/(17·12)+ 1/(577·408) + …)
Mit den ersten 3 Summanden erhält man als Näherung 1,41421356237… (√2 = 1,41421356237310…) mit elf exakten Ziffern. Berücksichtigt man x3 = 665857, y3 = 470832 stimmt der Näherungswert auf 21 Stellen.
Umgekehrt kann mittels Kettenbruchentwicklung der Quadratwurzel auch die Pellsche Gleichung gelöst werden.
Dazu entwickelt man √D in einen Kettenbruch und wählt an, die vorletzte Zahl einer Periode. Ist die Länge der Periode ungerade, so nutzt man die vorletzte Zahl der zweiten Periode.
Ist [a1, a2, a3, …] der Kettenbruch, so ermittelt man den n.ten Näherungsbruch pn / qn. Dazu verwendet man p0 = 1, q0 = 0, p1 = a1 und q1 = 1:
pn = an pn-1 + pn-2 ; qn =an qn-1 + qn-2
Das Paar x = pn und y = qn ist dann eine Lösung der Gleichung.
Beispiel: x² – 7y² = 1
Die Kettenbruchentwicklung von √7 ist [2; 1, 1, 1, 4, 1, 1, 1, 4 …].
Die vorletzte Zahl der ersten Periode ist a4 = 1 und der 4.Näherungsbruch ist 8/3. x = 8 und y = 3 sind also Lösung der Gleichung, denn 8² – 7·3² = 1.
Eine weitere Lösung erhält man aus a8, der vorletzten Zahl der zweiten Periode, der 8.Näherungsbruch ist 127/48, und 127² – 7·48² = 1.
Zur Umwandlung einer Quadratwurzel in einen periodischen Kettenbruch kann folgender Algorithmus verwendet werden:
function kettenbruchwurzel(a:integer):string;
var x,a1,b1,e:integer;
ausgabe:string;
begin
x:=trunc(sqrt(a+0.01));
ausgabe:=’[’ +inttostr(x) + ’, ’;
a1:=x;
b1:=a1;
e:=a-a1*a1;
if (e>0) then begin
while (a1<>2*x) do begin
a1:=(x+b1) div e;
ausgabe:= ausgabe + inttostr(a1) + ’; ’;
b1:= a1*e-b1;
e:=(a-b1*b1) div e;
end
end;
result:=ausgabe +’]’;
end;
Quelle: Khinchin, Continued fractions, Dover Publications New York 1997
| Pellsche Gleichung | |
|---|---|
 |
|
| Herunterladen | |
Download
Die Berechnung der Pellschen Gleichung ist hier auch als Programm downloadbar.
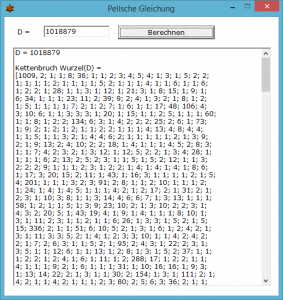
Das angehängte Programm berechnet für alle D ≤ 6938778 den Kettenbruch von √D und die kleinste Lösung der entsprechenden Pellschen Gleichung.
Für D = 6938779 überschreitet die Periode des Kettenbruchs mit einer Länge von 7616 die im Moment vorgesehenen 7500 Glieder.
John Pell
Pell befasste sich mit Diophantische Gleichungen. Die spezielle diophantische Gleichung
X² – D Y² = 1
(wobei d eine ganze Zahl ist, die kein Quadrat ist) ist zwar als Pellsche Gleichung bekannt, war aber schon den mittelalterlichen, indischen Mathematikern Brahmagupta und Bhaskara II. bekannt.
Die Lösung dieser Gleichung war als Problem von Pierre de Fermat in einem Brief an Bernard Frénicle de Bessy gestellt worden und 1657 als Problem zur allgemeinen Kenntnis veröffentlicht. Die Theorie der Gleichung erst im 18. Jahrhundert von Joseph-Louis Lagrange entwickelt.
Pells Beziehung zu dem Problem lag lediglich in der Publikation der Lösungen von John Wallis und William Brouncker in der englischen Übersetzung der Algebra von Rahn (1668).