Höhensatz, Kathetensatz, Satz des Pythagoras
„Kandidat: ‚a² + b² = c².‘
G. Jauch: ‚Ist das nicht die binomische Formel?’“
RTL-Quizshow am 7.10.2002
 Obwohl die mathematische Bildung der Bevölkerung in Deutschland im Vergleich zu anderen Industrienationen verheerend ist, können zumindest viele wenigstens einen mathematischen Satz nennen: den Satz des Pythagoras. Zwar wird dieser immer in der verkürzten Form a² + b² = c² genannt, ohne zu wissen, was er wirklich aussagt, aber immerhin ist dies ein Anfang!
Obwohl die mathematische Bildung der Bevölkerung in Deutschland im Vergleich zu anderen Industrienationen verheerend ist, können zumindest viele wenigstens einen mathematischen Satz nennen: den Satz des Pythagoras. Zwar wird dieser immer in der verkürzten Form a² + b² = c² genannt, ohne zu wissen, was er wirklich aussagt, aber immerhin ist dies ein Anfang!
Drei Sätze am rechtwinkligen Dreieck, der Höhensatz, der Kathetensatz oder Satz des Euklid und der Satz des Pythagoras, gehören seit rund 2500 Jahren zum mathematischen Wissen. Ihre Berühmtheit erlangten diese mathematischen Gesetze aufgrund ihrer einfachen Struktur und inneren Schönheit. Schon die Pythagoräer waren, gemäß ihres Kernsatzes „Alles ist Zahl“, von der Möglichkeit, geometrische Zusammenhänge mittels einfacher Zahlen auszudrücken, begeistert. Allerdings war der nach Pythagoras benannte Satz schon lange vorher im antiken Babylon (etwa 1600 v.u.Z.) bekannt.
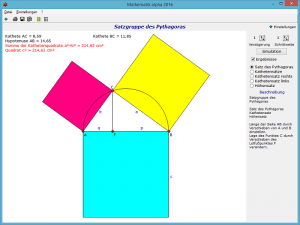
Das Teilprogramm Satzgruppe des Pythagoras in der Auswahl geometrischer interaktiver Programmteile gibt Ihnen die Möglichkeit, diese drei Sätze geometrisch zu veranschaulichen und zu untersuchen.
Nach Auswahl des Satzes an den Auswahlfeldern stellen Sie die Größe der Hypotenuse AB des Dreiecks durch Verschieben der Punkte A und B ein. Die Lage des dritten Dreieckspunktes C verändern Sie, indem Sie mit der Maus den Lotfußpunkt F längs der Hypotenuse verschieben.
Das Programm stellt Ihnen sofort den entsprechenden Satz dar und berechnet die wichtigen Größen. Für den Kathetensatz können Sie zusätzlich entscheiden, ob die linke oder rechte Seite der Figur gezeichnet wird.
Insgesamt finden Sie:
- Höhensatz: Im rechtwinkligen Dreieck ist das Quadrat über der Höhe auf der Hypotenuse flächengleich mit dem Rechteck aus den Längen der Hypotenusenabschnitte.
- Kathetensatz oder Satz des Euklid: Im rechtwinkligen Dreieck ist das Quadrat über einer Kathete flächengleich dem Rechteck aus der Länge der Hypotenuse und der Länge der Projektion dieser Kathete auf die Hypotenuse.
- Satz des Pythagoras: Im rechtwinkligen Dreieck ist die Fläche des Quadrats über der Hypotenuse gleich der Summe der Flächen der Quadrate über den Katheten.
| Satz des Pythagoras |
|---|
 |
| Herunterladen |
Die Simulation bewirkt stets eine kontinuierliche Verschiebung des Höhenfußpunktes von links nach rechts.
Download
Ein Einzelprogramm zum Satz des Pythagoras, in anderer Form als in „Mathematik alpha“ steht hier zum Download bereit.
Satz des Pythagoras
Die „Elemente“ (griechisch: stoicheia) sind das klassische Geometriewerk von Euklid.
Die „Elemente“ waren für mehr als 1000 Jahre das grundlegende Geometrielehrbuch in Europa und erschien im Laufe der Geschichte in über 2000 Auflagen.

Sie beginnen mit 23 Grunddefinitionen und 5 geometrischen Postulaten. Mit Hilfe dieser Postulate gelingt es Euklid, die geometrischen Aussagen seiner 13 Bücher herzuleiten und zu begründen.
Der Text enthält den Beweis von Euklid für den Satz des Pythagoras in den „Elementen“.
Am rechtwinkligen Dreieck ist das Quadrat über der dem rechten Winkel gegenüberliegenden Seite den Quadraten über den den rechten Winkel umfassenden Seiten zusammen gleich.
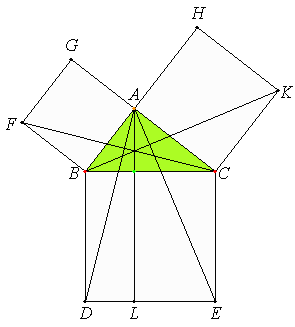 A B C sei ein rechtwinkliges Dreieck mit dem rechten Winkel B A C. Ich behaupte, dass B C² = B A² + A C².
A B C sei ein rechtwinkliges Dreieck mit dem rechten Winkel B A C. Ich behaupte, dass B C² = B A² + A C².
Man zeichne nämlich über B C das Quadrat B D E C (I, 46) und über B A, A C die Quadrate G B, H C; ferner ziehe man durch A A L || B D oder C E und ziehe A D, F C.
Da hier die Winkel B A C, B A G beide Rechte sind, so bilden an der geraden Linie B A im Punkte A auf ihr die zwei nicht auf derselben Seite liegenden geraden Linien A C, A G Nebenwinkel, die zusammen = 2 R. sind; also setzt C A A G gerade fort (I, 14). Aus demselben Grunde setzt auch B A A H gerade fort.
Ferner ist ∠ D B C = F B A; denn beide sind Rechte (Postulat 4); daher füge man A B C beiderseits hinzu; dann ist der ganze Winkel D B A dem ganzen F B C gleich (Axiom 2). Da ferner D B = B C und F B = B A (I, Definition 22), sind die zwei Seiten D B, B A zwei Seiten F B, B C überkreuz entsprechend gleich; und ∠ D B A = ∠ F B C; also ist Grundlinie A D = Grundlinie F C und Δ A B D = Δ F B C (I, 4).
Ferner ist Parallelogramm B L = 2 Δ A B D; denn sie haben dieselbe Grundlinie B D und liegen zwischen denselben Parallelen B D, A L (I, 41); auch ist das Quadrat G B = 2 Δ F B C; denn sie haben wieder dieselbe Grundlinie, nämlich F B, und liegen zwischen denselben Parallelen F B, Q C. Von Gleichem die Doppelten sind aber einander gleich (Axiom 5). Also ist Parallelogramm B L = Quadrat G B.
Ähnlich lässt sich, wenn man A E, B K zieht, zeigen, dass auch Parallelogramm C L = Quadrat H C; also ist das ganze Quadrat B D E C den zwei Quadraten G B + H C gleich (Axiom 2). Dabei ist das Quadrat B D E C über B C gezeichnet und G B, H C über B A, A C. Also ist das Quadrat über der Seite B C den Quadraten über den Seiten B A, A C zusammen gleich. – S.
Koordinaten am rechtwinkligen Dreieck
Die Figur zum Satz des Pythagoras ist eine beliebte Programmieraufgabe für Anfänger.
Möchte man die Figur darstellen, so benötigt man die Koordinaten einer Vielzahl von Punkten. Unter Anwendung von Höhensatz, Kathetensätze und Ähnlichkeitsbetrachtungen ergibt sich:
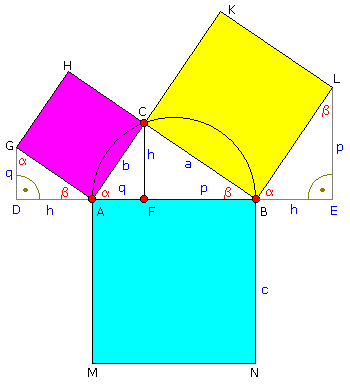 Ausgehend von den Seitenlängen a und b eines rechtwinkligen Dreiecks und der Lage des Punktes A im Ursprung wird:
Ausgehend von den Seitenlängen a und b eines rechtwinkligen Dreiecks und der Lage des Punktes A im Ursprung wird:
| A (0 ; 0) | B (c ; 0) | C (q ; h) |
| F (q ; 0) | D (-h ; 0) | E (c+h ; 0) |
| G (-h ; q) | H (-h+q ; q+h) | L (c+h ; p) |
| K (c+h-p ; p+h) | M (0 ; -c) | N (c ; -c) |
Zusammenhänge zwischen a, b und c, h, p und q
| a² + b² = c² p + q = c a² = p c b² = q c p q = h² |
Für den Satz des Pythagoras existieren sehr viele unterschiedliche Beweise. Der nachfolgende Text enthält rund 50 solcher Beweise.
Pythagoras-Gedicht
Ich weiß nicht, was soll es bedeuten,
Dass ich so traurig bin.
Ein Lehrsatz aus alten Zeiten,
Der kommt mir nicht aus dem Sinn.
Drei Winkel, wovon ein rechter,
Sind mit drei Seiten verwandt.
Und diese noblen Geschlechter
Regieren Leut‘ und Land.
Die schönste der Hypotenusen
Thront oben wunderbar.
Es schlummert an ihrem Busen
Ein holdes Kathetenpaar!
Sie thront auf hohem Quadrate
Und singt ein Lied dabei,
Das hat eine pythagorate
Gewaltige Melodei.
Der Welt unendlich Getriebe
Ergreift es mit wildem Weh,
Sie schwärmt in glühender Liebe
Für a², b², c!
Sogar die kühlen Kometen
Erfasst ein feuriger Wahn, –
Und das hat mit ihren Katheten
Die Hypotenuse getan.
Verfasser unbekannt, frei nach Heinrich Heine