Eine interessante Simulation wird in der Literatur als Ameisensimulation bezeichnet.
Chris Langtons Ameise ist eine Turingmaschine mit einem 2-dimensionalen Speicher, mit sehr einfachen Regeln und sehr verblüffenden Ergebnissen. Nach ihrem Erfinder werden diese Ameisen auch Langton-Ameisen genannt.
Zu Beginn befindet sich die „Ameise“ auf einer theoretisch unbegrenzten weißen Zeichenfläche und bewegt sich um einen Punkt vorwärts. Hat der erreichte Punkt eine weiße Farbe, färbt die Ameise den Punkt schwarz und wendet sich um 90° nach links. Ist der Punkt schwarz, wird er weiß gefärbt und die Ameise dreht sich um 90° nach rechts.
Wählen Sie die Programmauswahl Simulationen, so können Sie diese Simulation testen. Das Programm enthält neben dem Standardmodell auch noch weitere Möglichkeiten. Geben Sie dazu an, wie viele Ameisen gleichzeitig und eventuell einfarbig laufen sollen. Maximal können Sie 12 Ameisen gleichzeitig betrachten.
Testen Sie diese Möglichkeiten. Sie werden sehen, dass jedes Modell seinen eigenen Reiz besitzt. Bei jedem Neustart ermittelt das Programm zufällig einen neuen Anfangspunkt. Abbrechen können Sie die Bewegung der Ameise mit ESC oder dem Abbruch-Schalter.
| Ameisensimulation |
|---|
 |
| Herunterladen |
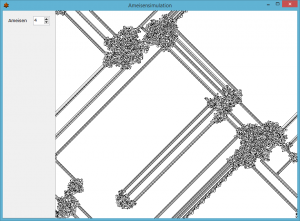
Das wirklich Interessante ist, dass die Ameise immer, allerdings kaum vorhersehbar wann, diagonal über den Bildschirm läuft. Chaotisches Verhalten schlägt in geordnetes um und umgekehrt. Die Ursache für so ein Verhalten ist bis heute noch nicht bekannt. Genauer gesagt kennt man noch keinen deterministisch polynomialen Algorithmus, mit dem bei gegebener Ausgangssituation das entstehende Bild ermittelt werden kann.
Anmerkung: Die Ameisen bewegen sich auf einer torusartigen Fläche, d.h., links und rechts sowie oben und unten sind miteinander verbunden. Verblüffend ist, dass dabei Darstellungen entstehen, die sich mitunter nach Tausenden von Schritten umkehren und alle gezeichneten Schritte bis zur Ausgangssituation wieder löschen.
Einfache programmtechnische Umsetzung
Zu Beginn befindet sich die „Ameise“ auf einer; theoretisch unbegrenzten; weißen Zeichenfläche und bewegt sich um einen Punkt vorwärts.
Hat der erreichte Punkt weiße Farbe, färbt die Ameise den Punkt schwarz und wendet sich um 90° nach links. Ist der Punkt schwarz, wird er weiß gefärbt und die Ameise dreht sich um 90° nach rechts.
Variablen: Richtung ri … integer; Koordinaten x,y … integer; paintbox1 Maße … breite, hoehe
Anfangswerte: zufällige Koordinaten x,y und zufällige Richtung ri
Delphi-Quelltext des Algorithmus:
repeat
if paintbox1.canvas.pixels[x,y]=$00ffffff then begin
paintbox1.canvas.pixels[x,y]:=$00;
dec(ri);
if ri=0 then ri:=4;
end else begin
paintbox1.canvas.pixels[x,y]:=$00ffffff;
inc(ri);
if ri=5 then ri:=1;
end;
case ri of
1 : inc(x);
2 : inc(y);
3 : dec(x);
4 : dec(y);
end;
if x<0 then x:=breite-1;
if x>breite-1 then x:=0;
if y<0 then y:=hoehe-1;
if y>hoehe-1 then y:=0;
application.processmessages
until abbruch;
Turk-Propp-Langton-Ameisen
Durch Greg Turk und Jim Propp wurde 1995 eine einfache, aber sehr interessante Erweiterung des klassischen Regelsystems der Langton-Ameisen beschrieben. Diese finden Sie im 2.Teilprogramm Langton-Ameisen.
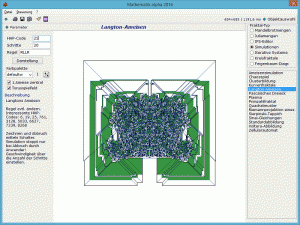
Anstelle der Langton-Rechts-Links-Regel RL werden nun Zyklen aus beliebigen R- und L-Bewegungen betrachtet und andersfarbig dargestellt. Mehrere Regeln erzeugen symmetrische Muster mit regelmäßigen und chaotischen Anteilen, z.B. RLLR. Die Abbildung zeigt die Regel LLRR.
Andere Bewegungsfestlegungen ergeben vollkommen chaotische Muster, manche nichts, wie z.B. LL und RR.
Voreingestellt ist die Regel LLRR (HHP-Code 19).
Interessante Regeln sind zum Beispiel: LLRR, RLLR, RLR, LRRRRRLLR, LLRRRLRLRLLR oder RRLLLRLLLRRR.
Zur Eingabe wird zuerst der HHP-Code verwendet; tragen Sie dort nichts ein, wird die Regel aus der dritten Eingabezeile entnommen.
Der HHP-Code wird zur systematischen Beschreibung der Regeln genutzt. Dazu werden die ‚L‘ und ‚R‘ einer Regel, z.B. ‚LRRL‘, als ‚0‘ und ‚1‘ interpretiert und die entstehende Dualzahl in das Dezimalsystem transformiert. Um führende ‚L‘ = ‚0‘ zu berücksichtigen, wird der Dualzahl eine 1 vorangestellt. Zum Beispiel wird ‚LRRL‘ damit zur Dualzahl 10110, d.h. 22 als Dezimalzahl. Jeder natürlichen Zahl größer 3 ist somit eine eindeutige Regel zugeordnet und umgekehrt.
| Turk-Propp-Langton-Ameisen | |
|---|---|
|
|
| Herunterladen | |
Bei der Berechnung wird eine torusförmige Spielfläche betrachtet. Möchten Sie das nicht, d.h. beim Erreichen der Bildränder stoppt die Animation automatisch, so entfernen Sie das Häkchen bei Toruspielfeld.
Die Berechnung und Darstellung wird hier mit möglichst großer Geschwindigkeit durchgeführt. Möchten Sie eine langsamere Darstellung, so tragen Sie unter Schritte eine kleinere Zahl ein; analog eine größere für eine schnellere Berechnung.