 Eine der auch heute noch interessantesten Aufgaben der Mechanik ist die Untersuchung des Verhaltens eines mathematischen Doppelpendels. Dabei ist ein Massekörper an einer masselosen Stange angebracht (Stangenpendel).
Eine der auch heute noch interessantesten Aufgaben der Mechanik ist die Untersuchung des Verhaltens eines mathematischen Doppelpendels. Dabei ist ein Massekörper an einer masselosen Stange angebracht (Stangenpendel).
Ein zweites Stangenpendel wird nun zusätzlich an dem ersten Massekörper befestigt. Beide Körper können unterschiedlich ausgelenkt werden.
Möchte man die Orte der Körper während der Schwingung wissen, wäre es notwendig, zwei Schwingungsdifferenzialgleichungen zu lösen. Extrem schwierig wird dies aber dadurch, dass sich der Aufhängepunkt der zweiten Schwingung selbst bewegt und durch die Verbindung beider Schwingungen eine ständige Energieübertragung stattfindet. Deshalb kann das Problem nicht mehr rein analytisch gelöst werden, sondern bedarf eines Näherungsverfahrens bzw. der Simulation mit dem Computer. Insbesondere zeigt sich, dass die Bewegung eines solchen Pendels extrem stark von den Anfangsbedingungen abhängig ist.
Dieses dynamische System besitzt Eigenschaften, die von der modernen Chaostheorie untersucht werden.
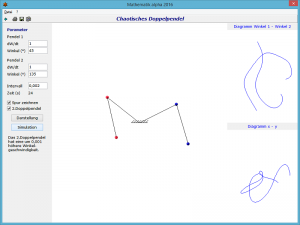
In diesem Unterprogramm wird das Verhalten eines solchen mathematischen Doppelpendels simuliert. Zu Beginn können Sie die Parameter der zwei Pendel wie folgt festlegen: Geben Sie in die Felder Winkel und dW/dt die Anfangswinkel und die schon vorgegebenen Winkelgeschwindigkeiten für beide Pendel ein. Die Darstellung des Pendels aktualisieren Sie mit dem Schalter Darstellung.
Im Eingabefeld Zeitintervall kennzeichnen Sie die Qualität der Berechnung und Darstellung.
Für die Berechnung der veränderlichen Orte beider Pendel benötigt das Programm ein Zeitintervall, mit dem das Näherungsverfahren arbeitet. Erhöhen Sie den Wert im Feld Zeitintervall, werden die neuen Orte in größeren Abständen ermittelt, d.h., die Berechnung und Darstellung werden fehlerbehafteter und damit ungenauer. Verringern Sie den Wert, erhalten Sie eine genauere Zeichnung. Allerdings steigen die Anforderungen an Ihren Computer. Auf einem Pentium mit geringer Taktfrequenz erwies sich der voreingestellte Wert von 0.002 s als optimal.
Während der Animation können Sie über das Schaltfeld Spur den zurückgelegten Weg des äußeren Massepunktes darstellen lassen. Das Programm zeichnet die Orte der letzten 1000 Berechnungen ein, d.h. bei einem Zeitintervall von 0.01 s den Weg in den letzten 10 Sekunden.
Mitunter führt das Doppelpendel scheinbar unregelmäßige Bewegungen aus. Anhand der Spur können Sie verfolgen, dass sich das Pendel oft längere Zeit annähernd gleichmäßig bewegt und dann plötzlich ein völlig anderen Weg nimmt. Dieses chaotische Verhalten führte auch zu der Bezeichnung „Chaospendel“ für dieses mathematische Doppelpendel.
Wählen Sie 2. Doppelpendel, so wird ein zweites chaotisches Doppelpendel berechnet. Dieses erhält zu Beginn eine um 1 / 1000 höhere Winkelgeschwindigkeit des äußeren Pendels.
| Chaotisches Doppelpendel |
|---|
 |
| Herunterladen |
Anfangs werden beide Pendel die gleiche Bahn beschreiben.
Allerdings ändert sich dies nach etwa 20 Sekunden – dann weichen beide deutlich voneinander ab. Eine kleine Änderung der Anfangsgrößen führt damit zu einer großen Wirkung.
Anmerkung: Im Forum Matheraum.de wurde durch „Al-Chwarizmi“ (Nutzername!) folgendes angemerkt:
„Würde man ein Doppelpendel wirklich durch zwei aneinander gehängte Fadenpendel realisieren, so erhielte man ein noch deutlich komplexeres System, da die beiden Fäden längst nicht immer gespannt wären und sich insbesondere die zweite Masse sehr oft auf Wurfparabeln bewegen würde (jeweils bis der Faden wieder gespannt ist).
Anstatt von Fadenpendeln sollte man also besser von „Stangenpendeln“ oder „Stabpendeln“ sprechen.“
Danke für den Hinweis. Der ursprüngliche Fehler wurde gern korrigiert.