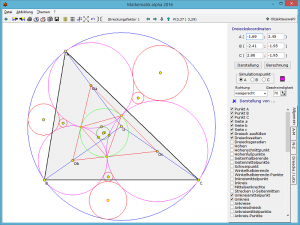
 Dieses Teilprogramm ist eines der komplexesten dieses Programms. Ausgehend von den drei Eckpunkten eines Dreiecks können Sie hier verschiedenste Punkte, Geraden und Kreise an einem beliebigen Dreieck darstellen und berechnen.
Dieses Teilprogramm ist eines der komplexesten dieses Programms. Ausgehend von den drei Eckpunkten eines Dreiecks können Sie hier verschiedenste Punkte, Geraden und Kreise an einem beliebigen Dreieck darstellen und berechnen.
Durch die Möglichkeit, die Lage der Dreieckspunkte A, B und C durch Anklicken und Verschieben mit der Maus zu verändern, ist die Untersuchung vielfältiger geometrischer Gebilde leicht möglich.
Die zu zeichnenden Punkte, Geraden und Kreise wählen Sie durch Markierung in der Liste aus. Zur besseren Orientierung sind alle Darstellungsobjekte in vier Listen eingeordnet. Dies sind:
- Punkte A, B und C … Die Eckpunkte des Dreiecks
- Seite a, b und c … Die Dreiecksseiten
- Dreiecksseiten … Die Seiten a, b und c werden deutlicher hervorgehoben
- Dreiecksgeraden … Die Geraden, welche die Verlängerung der Dreiecksseiten darstellen
- Höhen … Die Höhen des Dreiecks, d.h. die von den Eckpunkten auf die gegenüberliegenden Seiten gefällten Lote
- Seitenhalbierende … Die Geraden durch die Eckpunkte und die Mittelpunkte der gegenüberliegenden Seiten
- Seitenmittelpunkte … Die Mittelpunkte der drei Seiten
- Mittelparallelen … Drei von den Seitenmittelpunkten gebildete Strecken, die jeweils zu einer Dreiecksseite parallel sind
- Winkelhalbierende … Die Geraden, welche die Innenwinkel des Dreiecks halbieren
- Winkelhalbierende-Punkte … Die Schnittpunkte der Winkelhalbierenden mit den gegenüberliegenden Seiten
- Mittelsenkrechte … Die Geraden, die in den Seitenmittelpunkten senkrecht auf den Dreiecksseiten stehen
- Höhenschnittpunkt … Der Schnittpunkt der drei Höhen
- Schwerpunkt … Der Schnittpunkt der drei Seitenhalbierenden, der zugleich der Schwerpunkt des Dreiecks ist
- Inkreismittelpunkt … Der Schnittpunkt der Winkelhalbierenden und zugleich der Mittelpunkt des Inkreises
- Inkreis … Der Kreis, der die drei Dreiecksseiten von innen berührt
- Umkreismittelpunkt … Der Schnittpunkt der Mittelsenkrechten und zugleich der Mittelpunkt des Umkreises
- Umkreis … Der Kreis, der durch die Eckpunkte des Dreiecks verläuft
- Ankreise … Drei Kreise, die jeweils eine Dreiecksseite und die anderen beiden Verlängerungen der Dreiecksseiten berühren, die sogenannten Kreise des Apollonius
- Ankreisdreieck … Das Dreieck, das von den drei Ankreismittelpunkten gebildet wird
- Ankreismittelpunkte … Die drei Punkte, welche die Mittelpunkte der Ankreise sind
- Ankreis-Punkte … Die drei Berührungspunkte der Ankreise an den eigentlichen Dreiecksseiten
- Euler-Gerade … Die Gerade, auf welcher der Höhenschnittpunkt, der Schwerpunkt, der Umkreismittelpunkt und der Feuerbach-Punkt liegen
- Feuerbach-Kreis … Ein Kreis, der neun besondere Punkte enthält: die drei Höhenfußpunkte, die drei Seitenmitten und die drei Mitten zwischen dem Höhenschnittpunkt und den Dreiecksecken
- Feuerbach-Punkt … Der Mittelpunkt des Feuerbach-Kreises, der auch auf der Eulerschen Geraden liegt
- 9-Feuerbach-Punkte … Die neun besonderen Punkte des Feuerbach-Kreises: die drei Höhenfußpunkte, die drei Seitenmitten und die drei Mitten zwischen dem Höhenschnittpunkt und den Dreiecksecken
- Soddy-Kreise … Drei Kreise um die Dreiecksecken, die sich paarweise berühren
- Höhenfußpunkte … Die Schnittpunkte der Höhen mit den Dreiecksseiten, die gleichzeitig die Lotfußpunkte von den Ecken zu den gegenüberliegenden Seiten sind
- Höhendreieck … Das Dreieck, das von den Höhenfußpunkten gebildet wird
- Inkreispunkte … Die Berührungspunkte des Inkreises
- Kontakt-Dreieck … Das von den Inkreisberührungspunkten gebildete Dreieck
- Lémoine-Punkt … Der Schnittpunkt der Symmedian-Linien
- Dreieck ausfüllen … Das Ausgangsdreieck wird gefärbt
Zusätzlich enthält das Programm Hunderte weitere darstellbare Objekte.
Wählen Sie einige Stücke aus, so können Sie zum Beispiel nachvollziehen, dass Höhenschnittpunkt, Feuerbach-Punkt, Schwerpunkt und Umkreismittelpunkt auf der Eulerschen Geraden liegen, dass der Spieker-Kreis auch Inkreis des Nagel-Halbdreiecks ist oder auch, dass die Soddy-Kreise durch die Inkreisberührungspunkte verlaufen usw. Dem Experimentieren sind kaum Grenzen gesetzt.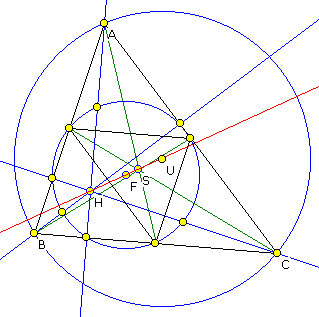 In der Abbildung wurden die Höhen, Seitenhalbierenden, der Höhenschnittpunkt, der Schwerpunkt, der Umkreismittelpunkt, der Umkreis, der Feuerbach-Kreis mit Mittelpunkt, die neun besonderen Feuerbach-Punkte, die Euler-Gerade und die Mittelparallelen eingezeichnet.
In der Abbildung wurden die Höhen, Seitenhalbierenden, der Höhenschnittpunkt, der Schwerpunkt, der Umkreismittelpunkt, der Umkreis, der Feuerbach-Kreis mit Mittelpunkt, die neun besonderen Feuerbach-Punkte, die Euler-Gerade und die Mittelparallelen eingezeichnet.
Neben der Möglichkeit, die Eckpunkte mittels Maus zu verschieben, können Sie die Koordinaten auch eingeben. Dabei wird davon ausgegangen, dass der Ursprung im Bildzentrum liegt. Veränderte Koordinaten quittieren Sie mit Darstellung oder Berechnung.
Achtung! Sollten Sie sehr viele Stücke oder sogar alle auswählen, wird die Darstellung vollkommen unübersichtlich. Hier gilt das alte Sprichwort: Weniger ist oft mehr!
Simulation der Bewegung der Dreieckspunkte
Auch in diesem Teilprogramm können Sie den Computer wieder veranlassen, eine Simulation durchzuführen. Dabei ist es möglich, die drei Eckpunkte A, B und C des Dreiecks entweder waagerecht, senkrecht, um den Ursprung kreisend oder in Richtung der Geraden AB kontinuierlich zu verschieben. Markieren Sie den entsprechenden Punkt und die Simulationsrichtung.
Berechnungen am Dreieck
Die zu zeichnenden Stücke können Sie auch berechnen lassen. Markieren Sie das Feld Berechnungsergebnisse, zeigt das Programm in einer Liste die Koordinaten der Punkte, Längen von Strecken und Gleichungen von Geraden an. Dabei werden die Koordinaten der Eckpunkte übernommen.
Koordinaten berechneter Punkte werden in dem üblichen kartesischen Koordinaten angezeigt. Sollen zusätzlich die trilinearen Koordinaten angegeben werden, dann wählen Sie die den entsprechenden Menüpunkt.
Wünschen Sie die Berechnung für andere Werte, so ändern Sie die Koordinaten der drei Eckpunkte und quittieren mit Berechnung. Um wieder zur Darstellung umzuschalten, markieren Sie einfach das entsprechende Feld.
Vordefinierte Themen
Aufgrund der großen Anzahl darstellbarer Objekte ist deren Auswahl nicht ganz so einfach. Aus diesem Grund sind unter dem Menüpunkt Themen 70 besondere Beziehungen am Dreieck vordefiniert. Wählen Sie einen der Punkte aus, so zeichnet das Programm die einzelnen Punkte, Geraden, Kreise …, die für dieses Thema besonderes relevant sind.
| Dreieck |
|---|
 |
| Herunterladen |
Download
Dieser Programmteil steht wieder als Einzelprogramm zum Download bereit.