Der Kupferstich „Melancholia“ von Albrecht Dürer enthält die Darstellung eines Polyeders, des Dürer-Polyeders, mit 8 Flächen. Dürer hat niemals diesen Körper genauer beschrieben.
Nach Schröder (1980) handelt es sich um einen Würfel der mit Rhomben erweitert wurde und anschließend an zwei gegenüberliegenden Ecken so abgeschnitten wurde, dass regelmäßige Dreiecke entstehen.
Der entstandene Körper setzt sich aus sechs gleichen, unregelmäßigen, achsensymmetrischen Fünfecken und zwei gleichseitigen Dreiecken zusammen. Er hat zwölf Ecken, an jeder Ecke treffen drei Flächen aufeinander. Alle Eckpunkte liegen auf derselben Umkugel. Gegenüberliegende Flächen sind parallel. Der Körper hat 18 Kanten.
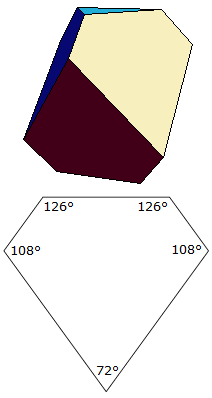Die entstehenden unregelmäßigen Fünfeckseiten haben die Innenwinkel 126°, 108°, 72°, 108° und 126° und die Seitenlängen verhalten sich wie
1 : 1/2 (3 +√5) : √(1/2 (5 + √5)) ≈
≈ 1 : 2,61803 : 1,90211
Ist a die Größe der langen Seiten, b die der anliegenden Seiten, c die obere, einzelne Seite, e = a/2 √(10 – 2 √5) die Diagonale und r = a – b der Umkreisradius des Fünfecks, so gilt
a : r = r : b = e : c = F (Verhältnis des goldenen Schnittes)
Volumen V = 5/3 a³ √(√5 – 2) ≈ 0,80978045 a³
Oberflächeninhalt A = a²/2 (3 √(5 + 2 √5)) + 5 √3 – 2 √15) ≈ 5,07366898 a²
Umkugelradius R = a/4 √(14 – 2 √5) ≈ 0,771681 a
Fünfeckfläche A5 = a²/4 √(5 + 2 √5) ≈ 0,7694209 a²
Dreiecksfläche A3 = a²/4 √3 (5 – 2 √5) ≈ 0,2285718 a²
Für das Dürer-Polyeder findet man folgende Koordinaten und Flächen, mit
C0 = 0,20569829…, Wurzel einer Lösung von 3176523 x³ – 432180 x² + 14112 x – 64 = 0
C1 = 0,34701607…, Wurzel einer Lösung von 1728 x³ – 576 x² + 36 x + 1 = 0
C2 = 0,35627989…, Lösung von 343 x³ + 98 x² – 56 x – 8 = 0
C3 = 0,35997200…, Wurzel einer Lösung von 1728 x³ – 720 x² + 72 x – 1 = 0
C4 = 0,41139658…, Wurzel einer Lösung von 3176523 x³ – 1728720 x² + 225792 x – 4096 = 0
C5 = 0,62348980…, Lösung von 8 x³ + 4 x² – 4 x – 1 = 0
C6 = 0,64445842…, Wurzel einer Lösung von 203297472 x³ – 233722944 x² + 50381604 x + 4826809 = 0
C7 = 0,71994401…, Wurzel einer Lösung von 27 x³ – 45 x² + 18 x – 1 = 0
Eckkoordinaten
(C2, C0, C6) (C2, -C0, -C6) (-C2, C0, C6) (-C2, -C0, -C6) (0, -C4, C6) (0, C4, -C6) (C5, C3, C1) (C5, -C3, -C1) (-C5, C3, C1) (-C5, -C3, -C1) (0, -C7, C1) (0, C7, -C1)
Flächen { 10, 4, 2, 8, 9 } { 10, 9, 3, 1, 7 } { 10, 7, 6, 0, 4 } { 11, 5, 3, 9, 8 } { 11, 8, 2, 0, 6 } { 11, 6, 7, 1, 5 } { 0, 2, 4 } { 1, 3, 5 }
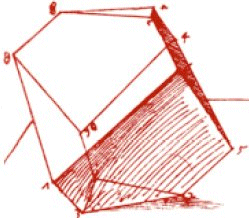Auf Dürers Stich ist das Polyeder ein an zwei Polyederecken abgestumpftes Rhomboeder (nach Schröder).
Dies geht aus einer Vorstudie hervor, in welcher auch die verdeckten Kanten eingezeichnet sind. Die Vorstudie ist spiegelbildlich zur Ausführung im späteren Stich. Dürer hatte in dieser perspektivischen Vorstudie auch den Augpunkt markiert.
Durch Schröder wurde auch ein Dreiseitenriss des Polyeders angegeben:
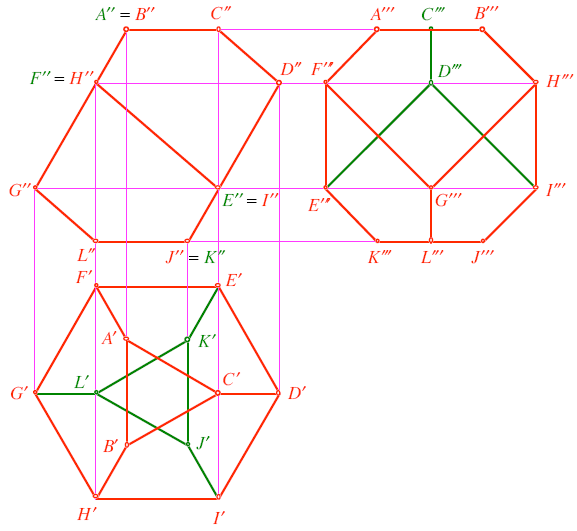
Dreiseitenriss des Dürer Polyeders
Das Polyeder hat als Seitenflächen zwei kongruente gleichseitige Dreiecke und sechs kongruente achsensymmetrische, aber nicht regelmäßige Fünfecke.
Es hat Punktsymmetrie, eine dreistrahlige Drehsymmetrie (Achse durch die beiden Dreiecksmitten), drei Achsen mit zweistrahliger Drehsymmetrie (Achsen durch Mittelpunkte gegenüberliegender langer Fünfeckskanten) und drei Symmetrieebenen.
Zum 300.Geburtstag Leonhard Eulers (1707-1783) veröffentlichte die schweizerische Post eine Briefmarke.
Die Sondermarke zeigt links ein Polyeder sowohl in massiver Form, aber auch als Kantenmodell. Die im massiven Modell sichtbaren Kanten sind im Kantenmodell rot gezeichnet, die unsichtbaren Kanten grün. Die grünen Kanten geben damit eine Information über die nicht sichtbare Rückseite des Polyeders. Das Polyeder dient als Illustration zur Eulerschen Polyederformel
e – k + f = 2
Das Polyeder ist offensichtlich aus Dürers Melancholia (1514) entnommen worden. Allerdings wurde die nicht sichtbare Rückseite nicht im Sinne Dürers interpretiert.
Auf Dürers Stich ist das Polyeder ein an zwei Polecken abgestumpftes Rhomboeder und hat zwei kongruente gleichseitige Dreiecke und sechs kongruente achsensymmetrische, aber nicht regelmäßige Fünfecke als Seitenflächen.
Auf der Briefmarke hat der Körper ein regelmäßiges Dreieck, drei achsensymmetrische Fünfecke, ein Rechteck, zwei kongruente Parallelogramme, zwei unregelmäßige, aber zueinander kongruente Vierecke als Seitenflächen.
Diese beiden Vierecke liegen in einer Ebene und könnten somit sogar zu einem Sechseck zusammengefasst werden. Die Kante zwischen diesen beiden Vierecken ist also eine unechte Kante. (nach Hans Walser)
Literatur:
1. Ritter, Tod und Teufel (Gloger, 1976, 238 Seiten, 20 MByte)
2. Albrecht Dürer und seine Zeit (1974, 52 Seiten, 21 MByte)
2. Schröder, „Dürer – Kunst und Geometrie“, Berlin Akademie-Verlag, 1980