Definition (Sloane): Eine natürliche Zahl z heißt fastprim n.Grades, wenn die Summe der Exponenten ihrer Primfaktorzerlegung gleich n ist, d.h. wenn
z = p1a1 · p2a2 · … · prar
die Primfaktorzerlegung ist und es gilt n = Σ ai . Eine fastprime Zahl 2.Grades heißt auch halbprim.
Beispiele:
| halbprim | 4, 6, 9, 10, 14, 15, 21, 22, … |
| 3.Grades | 8, 12, 18, 20, 27, 28, 30, 42, 44, 45, 50, 52, 63, 66, 68, 70, … |
| 4.Grades | 16, 24, 36, 40, 54, 56, 60, 81, 84, 88, 90, 100, … |
| 5.Grades | 32, 48, 72, 80, … |
Alle Quadratzahlen und Zahlen, welche genau aus zwei Primfaktoren zusammengesetzt sind, sind halbprim bzw. semiprim. Primzahlen sind nach der Definition „fastprime Zahlen 1.Grades“.
Fastprime Quadrupel
In Analogie zu den Primzahlvierlingen kann man auch nach Quadrupeln suchen, die innerhalb eines Zehners auf 1, 3, 7 und 9 enden, und alle fastprim zu einer bestimmten Ordnung sind,
d.h. gesucht sind 4 fastprime Zahlen n.Grades der Form
a · 10x + 1, a · 10x + 3, a · 10x + 7, a · 10x + 9
für natürliche a und n.
Die kleinsten fastprimen Zahlen, ab denen ein derartiges Quadrupel beginnt, sind
| n | |
| 2 | 321, 1921, 1961, 2321, … |
| 3 | 21091, 25201, 27861, 30651, … |
| 4 | 1911531, 2202231, 2460931, 2466451, … |
| Fastprime Quadrupel |
|---|
 |
| Herunterladen |
| 64-Bit-Programm |
| Herunterladen |
Download
Fastprime Quadrupel 2.Grades können mit etwas Aufwand auch für größere Zahlen gesucht werden.
Das hier downloadbare kleine Programm sucht ab der eingegebenen Zahl nach dem nächsten derartigen Quadrupel.
Die Wahl des maximalen Größe des kleinen Faktors entscheidet über die Geschwindigkeit der Berechnung. Kleinere Faktoren finden nicht unbedingt das nächste Quadrupel nach der Startzahl.
Die Berechnung kann auch für kleinere Startzahlen sehr lange dauern. Dagegen kann für große Anfangswerte auch zufällig sehr schnell ein Ergebnis erzielt werden.
Das 2. downloadbare Programm ist ein mit Lazarus erstelltes 64-Bit-Programm, dessen Berechnungsgeschwindigkeit gegenüber dem 32-Bit-Programm i.A. etwa 30 % schneller ist.
Besonderer Dank gilt Horst_H und Gammatester, die den Algorithmus des Programms deutlich verbesserten.
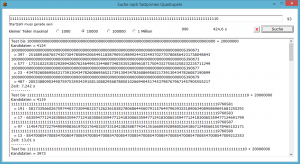
Zum Beispiel findet man für die 36stellige Startzahl 111111111111111111111111111111111111 das Quadrupel:
111111111111111111111111111111675401
= 251 · 442673749446657813191677733512651
111111111111111111111111111111675403
= 17 · 6535947712418300653594771241863259
111111111111111111111111111111675407
= 389 · 285632676378177663524707226508163
111111111111111111111111111111675409
= 7 · 15873015873015873015873015873096487
Das durch den Autor gefundene größte 402stellige Quadrupel beginnt bei 10401 + 221472831 und hat die kleinen Teiler 911, 3, 29, 3 der vier Quadrupelzahlen.
Durch hyperG wurde ein 700stelliges Quadrupel gefunden. Dessen erste Zahl ist 3000…00077614211.
Die nachfolgende Datei enthält die kleinsten fastprimen Quadrupel für Startzahlen 10m , vollständig bis m ≤ 403 (Stand: 16. August 2017). Besonderer Dank gilt Horst_H für die Berechnung der Werte ab 310: