Dreidimensionale Funktionen (Flächenfunktionen) der Form
z = f(x,y)
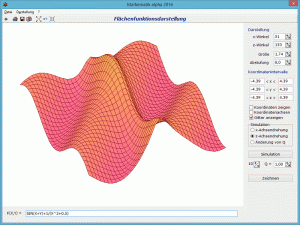
d.h. Funktionen, welche Flächen im dreidimensionalen Raum als Funktionsdarstellung haben, können in diesem Unterprogramm definiert und untersucht werden. Der Funktionswert Z ist hier von zwei Variablen X und Y abhängig. Für die grafische Darstellung bietet sich ein dreidimensionales Koordinatensystem an. Derartige Funktionen bilden dabei im Allgemeinen gekrümmte Flächen.
Beispiele: z = sin(xy) , z = x + y x²
Die Graphen der Funktionen werden dazu in einem Koordinatenwürfel dargestellt.
Eine veränderte Funktionsgleichung tragen Sie evtl. unter F(X,Y) = ein und quittieren mit dem Schalter Zeichnen.
Die Lage der Koordinatenachsen und damit die Ansicht der Funktion können Sie durch Änderung der Werte x-Winkel und z-Winkel erreichen. Außerdem können Sie mit einem linken Mausklick auf die Darstellung und das Bewegen der Maus, die Lage des Würfels beeinflussen.
Die Intervallgrößen der drei Koordinatenachsen tragen Sie in die entsprechenden Eingabezeilen ein. Die Farbe des Funktionsgraphen kann durch Klick auf einen der Menüpunkte Darstellung | Farbe 1 bzw. Darstellung | Farbe 2 oder die farbigen Rechtecke verändert werden. Ausgewählt wird die Farbe nach der Größe des Funktionswertes f(x,y).
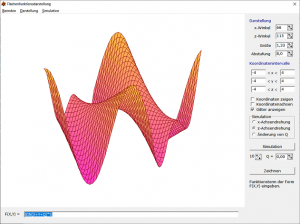
Mittels Schalter Simulation starten und stoppen Sie eine Simulation, bei der der Koordinatenwürfel kontinuierlich wahlweise um die x- oder z-Achse gedreht wird. Damit können Sie die Anschaulichkeit erhöhen.
Flächenfunktionen können in ihrer Funktionsgleichung einen Parameter Q enthalten. Dessen Wert können Sie an einem weiteren Rollbalken ändern.
| Flächenfunktionen |
|---|
 |
| Herunterladen |
Zusätzlich besteht auch die Möglichkeit, Q während der Simulation kontinuierlich im Intervall [-10 ; 10] ändern zu lassen. Das Programm zeichnet jeweils die Funktion und demonstriert so den Einfluss des Parameters Q. Die Geschwindigkeit der Änderung von Q kann an dem Rollbalken links vom Eintrag Q = verändert werden. Ein kleiner Wert verlangsamt die Änderung, ein hoher beschleunigt die Darstellung.