Geldwechsel-Problem

Gegeben sei eine Währung mit Münzen in der Größe 1, 5, 10, 25 und 50 Kreuzer.
Die größere Währungseinheit sei der Taler, der den gleichen Wert wie 100 Kreuzer besitzt.
Das Geldwechsel-Problem fragt nun, wie viele verschiedene Möglichkeiten es gibt, einen Taler in Kreuzer-Münzen zu wechseln.
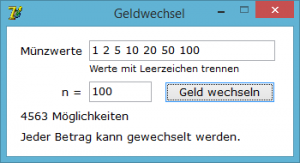
Schon für kleinere Beträge als 1 Taler existieren viele Möglichkeiten; für einen Taler 292 Varianten. Möchte man mit Euro-Münzen (1, 2, 5, 10, 20, 50 und 100 Cent) 1 Euro wechseln, so ist dies auf 4563 Fällen möglich.

Das Problem kann auf k Münzen beliebiger Größe m₁, m₂, m₃, …, m_k und einer zu wechselnden Betrag n verallgemeinert werden.
Um sicherzustellen, dass jeder Geldbetrag n gewechselt werden kann, sollte m₁ = 1 Einheit (Kreuzer) sein.

Allgemein besteht damit die Aufgabe, die Anzahl der Lösungen (a₁,a₂,a₃,…,a_k) der diophantischen Gleichung

a₁ · m₁ + a₂ · m₂ + a₃ · m₃ + … + a_k · m_k = n

zu finden.
Am einfachsten ist dies mittels Computersimulation möglich.

Brute-Force-Lösung

Bei diesem Verfahren werden alle möglichen Tupel (a₁,a₂,a₃,…,a_k) konstruiert und geprüft, ob die Summe gleich dem Zielwert n ist.
Für das Ausgangsproblem mit den Münzen 1, 5, 10, 25 und 50 und dem Zielwert n = 100, ist die umsetzbar mit folgendem Delphi-Text:

procedure TForm1.Button1Click(Sender: TObject);
const n=100;
var a1,a5,a10,a25,a50,anz:integer;
begin
   anz:=0;
   for a1:=0 to n do
       for a5:=0 to n div 5 do
           for a10:=0 to n div 10 do
               for a25:=0 to n div 25 do
                   for a50:=0 to n div 50 do
                       if a1+5*a5+10*a10+25*a25+50*a50=n then inc(anz);
   // Ausgabe der Größe von anz
end;

Rekursive Lösung

Eleganter ist eine rekursive Programmierung. Dazu werden die Münzwerte in einem Feld m gespeichert und die Funktion anz(n,k) rekursiv aufgerufen.
Der Rekursion wird  anz = anz(n,k-1) + anz(n-m[k],k) übergeben, d.h. kann die k.te Münze nicht mehr verwendet werden, der Betrag n und eine Münze weniger (k-1), sowie im Fall, dass die k.te Münze zum Wechsel genutzt wird, der nun um diese Münze reduzierte Restbetrag n-m[k] mit einem weiteren Versuch, die k.te Münze zu nutzen.

var m : array[1..100] of integer;
function anz(n,k: integer): integer;
begin
   if (n < 0) or (k = 0) then anz := 0
       else if n = 0 then anz := 1
           else anz := anz(n,k-1) + anz(n-m[k],k);
end;
procedure Geldwechsel;
var a,n,k : integer;
begin
   n := 100; //Zielwert eingeben
   m[1]:=1; m[2]:=5; m[3]:=10; m[4]:=25; m[5]:=50; //evtl. weiter
   k := 5; //Anzahl der Münzen
   a := anz(n,k);
   // Ausgabe der Möglichkeiten a
end;

Mathematische Lösung

Für eine mathematische Lösung muss die diophantische Gleichung

a₁ · m₁ + a₂ · m₂ + a₃ · m₃ + … + a_k · m_k = n

und für das Ausgangsproblem a + 5 b + 10 c + 25 d + 50 e = 100 untersucht werden. Dies ist mittels Fallunterscheidung möglich.

1.Fall e = 2 … ergibt 1 Lösung mit 2 x 50 Kreuzern

2.Fall e = 1 … d.h. a + 5b + 10c + 25d = 50
2.1.  d = 2 … ergibt 1 Lösung mit 1 x 50 und 2 x 25

2.2.  d = 1 … d.h. a + 5b + 10c = 25
hier kann c die Werte 2,1,0 annehmen.
für c = 2 wird a + 5b = 5 mit 2 Lösungen für (a,b) = {(5,0),(0,1)}
für c = 1 wird a + 5b = 15 mit 4 Lösungen für
(a,b) = {(15,0),(10,1),(5,2),(0,3)}
für c = 0 wird a + 5b = 25 analog 6 Lösungen für (a,b)

2.3.  d = 0 … a + 5b + 10c = 50 (analog zu oben)
mit c = 5,4,…,1,0 und 1, 3, 5, 7, 9, 11 Lösungen = 36 Lösungen

3.Fall e = 0 … a + 5b + 10c + 25 d = 100
3.1.  d = 4 … 1 Lösung
3.2.  d = 3 … analog zu oben, 12 Lösungen
3.3.  d = 2 … analog zu oben, 36 Lösungen
3.4.  d = 1 … analog zu oben, 72 Lösungen
3.5.  d = 0 … analog zu oben, 121 Lösungen

In der Summe ergeben sich die 292 Lösungen, die auch von den Computerprogrammen ermittelt werden.

Geldwechsel-Problem
Herunterladen

Das hier downloadbare Programm ermittelt nach der Eingabe des Zielwertes und der zur Verfügung stehenden Münzen die Anzahl der Wechselmöglichkeiten.
Außerdem wird die Frobenius-Zahl berechnet.

Danke an Siegfried Beyer für das erstellte Programm. Die ZIP-Datei enthält außer dem ausführbaren Programm auch den Delphi-Quelltext.