Zu den interessantesten Operationen an mathematischen Objekten gehört die Inversion am Kreis. Während Sie in mehreren Teilprogrammen Punkte, Geraden, Kreise usw. invertieren können, ist dies auch für komplexere Punktmengen, wie zum Beispiel mathematische Kurven, möglich. Die dabei entstehenden invertierten Kurven haben zum Teil ein verblüffendes Aussehen.
Nach Jakob Steiner (1830) gilt: Gegeben sei ein Kreis K mit dem Mittelpunkt O, dem Zentrum der Inversion, und dem Radius r. Ein Punkt P sei von O verschieden. Dann ist der zu P inverse Punkt P‘ derjenige auf dem Strahl OP, der von O die Entfernung OP‘ = r² / OP besitzt.
Eine Inversion vertauscht das Innere des Kreises K mit dem Äußeren. Die einzigen Punkte, die unverändert bleiben, sind die auf der Kreisperipherie liegenden Punkte.
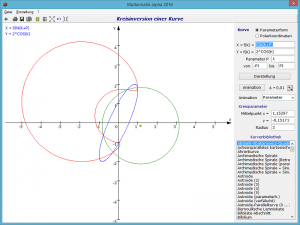
Zunächst muss die zu untersuchende Kurve eingegeben werden.
Die Größen des Kreises, d.h. die Lage des Mittelpunktes und die Größe des Radius, tragen Sie ebenfalls in die Eingabezeilen ein. Zusätzlich können Sie den Kreismittelpunkt (kleiner gelber Kreis) auch mit der Maus verschieben.
Die Größe des Darstellungsintervalls steuern Sie über den entsprechenden Schalter wie gewohnt. Klicken Sie auf den Schalter Animation, so wird für parameterhaltige Funktionen erneut die Größe des Parameters P kontinuierlich verändert. Ob P steigt oder sinkt, können Sie an den zwei kleinen Pfeilschaltern auswählen, ebenso die Stärke der Änderung Δ.
| Kreisinversion von Kurven |
|---|
 |
| Herunterladen |
Alternativ kann auch der Inversionskreis waagerecht bzw. senkrecht im Koordinatenkreis verschoben werden. Wählen Sie dies an den Auswahlfeldern.
Auch hier ergeben sich die merkwürdigsten Gebilde. Invertieren Sie zum Beispiel eine Astroide, ergibt sich eine Epizykloide. Das inverse Bild einer Hyperbel kann eine Lemniskate, eine Strophoide, aber auch eine Zissoide sein usw. usf. Dem Experimentieren und Staunen sind hier keine Grenzen gesetzt.