Der große deutsche Mathematiker und Astronom Johannes Kepler veröffentlichte 1619 sein Hauptwerk „Harmonices mundi“.
Im 2. Buch, dem „Architektonischen oder dem auf der figürlichen Geometrie beruhenden Buch“, untersucht Kepler die Kongruenz der „harmonischen Figuren“. Damit wird der Fragestellung nachgegangen, inwieweit reguläre Figuren die Ebene um einen festen Punkt herum lückenlos ausfüllen oder geschlossene Raumfiguren bilden können. Bei den räumlichen Kongruenzen führt Kepler zwei Sternpolyeder ein, die er als vollkommene reguläre Kongruenzen auffasst. Eines der beiden Sternpolyeder ist das kleine Sterndodekaeder.
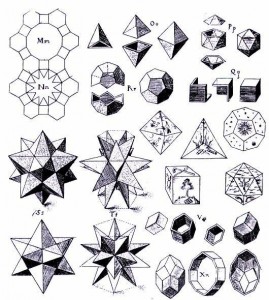Das kleine Sterndodekaeder oder zwölfeckige Sternzwölfflach besitzt als Seiten zwölf kongruente regelmäßige Sternfünfecke, die zu je fünf an jeder Ecke zusammentreffen. Das Polyeder hat 12 Seitenflächen, 12 Ecken und 30 Kanten. Netz des Sterndodekaeders
Die Eckpunkte stimmen mit den Eckpunkten des Ikosaeders überein. Zur Konstruktion des kleinen Sterndodekaeders beginnt man daher mit den zwölf Eckpunkten des Ikosaeders.
Die 30 Kanten entstehen durch Verbinden einer Ecke mit den fünf der Ecke nächstliegenden Eckpunkten. Je fünf dieser Kanten liegen in einer Ebene senkrecht zu einer Eckpunkt-Eckpunkt-Achse des Ikosaeders und bilden in dieser Ebene ein reguläres Sternfünfeck. Diese Sternfünfecke sind die Seiten des kleinen Sterndodekaeders. Die Symmetriegruppe entspricht der Ikosaeder-Gruppe A5.
Die Euler-Charakteristik ist -6, d.h. das nicht konvexe Polyeder entspricht nicht dem Eulerschen Polyedersatz.
Das rechte Bild zeigt ein schönes Modell des Sterndodekaeders.
Dabei wurde von Stefan Schwarz ein Pappmodell gebaut und mit 60 Dreiecksscheiben überklebt.
Weitere interessante Modelle sind auf der Seite „Holzpolyeder – Ideen zum Selberbauen“ zu finden.
Ist die Seitenlänge der Fünfecke am Grund einer „Spitze“ gleich a, so wird
| Oberfläche | A = 15 √(5 + 2 √5) a² ≈ 46,1652 a² |
| Volumen | V =5/4 (7 + 3 √5) a3 ≈ 17,1352 a3 |
Die Höhe der Spitzen; auf einem Dodekaeder der Seitenlänge a errichtet; ist
| Höhe | h = √(1 + 2/5 √5) a ≈ 1,37638 a |
Künstlerische Darstellungen
Das kleine Sterndodekaeder wurde auch von Künstlern in verschiedenen Werken genutzt.
Eines der berühmtesten ist „Gravitation“ von dem niederländischen Grafiker M.C.Escher.
Die 29,7 × 29,7 cm große Lithografie wurde 1952 zuerst schwarz-weiß gedruckt, später mit Wasserfarben nachkoloriert. Jede Seite des Sterndodekaeders hat eine halbrechteckige Tür. Aus diesen Türen ragen die Füße von 12 Schildkröten, die das Sterndodekaeder als gemeinsamen Panzer benutzen.
Die Schildkröten sind in sechs verschiedenen Farben entgegengesetzt dargestellt.
Eine Darstellung des Polyeders findet man als Mosaik (1430, Paolo Uccello) im Eingangsbereich von San Marco (Venedig).
Dieses Polyeder ist das „schönste Polyeder aller Zeiten“. Es vereint Mathematik mit Kunst und Schönheit.
Und daher ist dieses Sternpolyeder das Icon des Mathematikprogramms „Mathematik alpha“.