Eine Abbildung eines Gebietes der komplexen Ebene 1 in ein Gebiet der komplexen Ebene 2 mittels einer komplexwertigen Funktion f(z) heißt konforme Abbildung, wenn die Schnittwinkel zweier beliebiger Kurven der Größe nach erhalten bleiben. Die durch eine analytische Funktion f(z) erzeugte Abbildung ist für alle Punkte z konform, für die die erste Ableitung nicht verschwindet.
Die stereographische Projektion der Gaußschen Zahlenebene auf die Riemannsche Zahlenkugel ist ein Beispiel für eine konforme Abbildung.
In diesem Programm werden die Bilder einer konformen Abbildung erzeugt.
Dazu wird in zwei Teilfenstern die komplexe Gaußsche Zahlenebene dargestellt. Das Ausgangsintervall liegt bei etwa [-1, 1] und [-i, i].
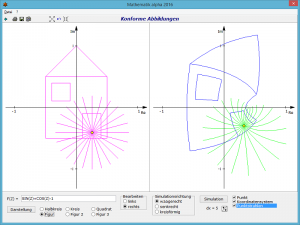
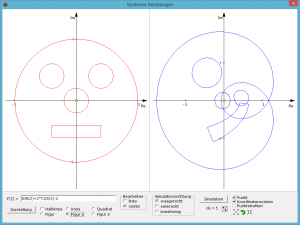
Im linken Teilfenster zeichnet das Programm, je nach Ihrer Wahl, ein Gitter in Form eines Halbkreises, Kreises oder Quadrates bzw. eine von drei vordefinierten Figuren. Alle Punkte dieses Gitters sind das Ausgangsgebiet der konformen Abbildung.
Unter F(Z) = tragen Sie eine komplexwertige Funktion ein. Beachten Sie bitte, dass das Argument der Funktion Z ist und folgende Funktionen und Operanden verwendet werden können:
- Standardfunktionen SQRT, SIN, COS, TAN, COT, SEC, CSC, SINH, COSH, TANH, COTH, EXP, LN
- Spezielle Funktionen GAMMA und die Besselschen Funktionen BI0, BJ0
- die Jacobischen elliptischen Funktion DN, SN, CN
- Exponentialintegral EI
- die Funktionen TRE(Z) und TIM(Z) für den Real- bzw. Imaginärteil des komplexen Arguments z
- Operanden +, -, *, / und die Potenzbildung ^
- Konstanten I, PI
Klicken Sie auf den Schalter Darstellung, wird das links dargestellte Gitter konform in das rechte Teilfenster abgebildet.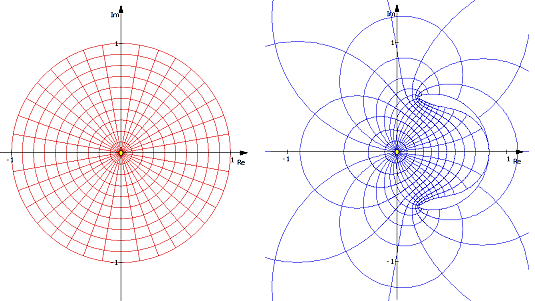
In der Darstellung wird ein Kreisgitter durch die Funktion f(z) = sin z / (z²+z-1) auf die rechte komplexe Ebene abgebildet.
Die Größe der rechten Darstellung können Sie über die Schalter in der oberen Schalterleiste des Fensters einstellen. Mitunter wirkt die Darstellung etwas „grob“. In diesem Fall können Sie am Rollbalken dx = die Feinheit der Zeichnung verändern. Ein kleinerer Wert verbessert die Darstellung, erhöht aber auch den Rechenaufwand.
Ist das Auswahlfeld Punkt markiert, wird im linken Koordinatensystem ein gelber Punkt angezeigt, den Sie mit der Maus verschieben können. Die konforme Abbildung dieses Punktes wird rechts ebenfalls angezeigt. Damit können Sie nachvollziehen, welcher Punkt wohin abgebildet wurde.
| Konforme Abbildungen |
|---|
 |
| Herunterladen |
Während der Simulation wird dieser Punkt kontinuierlich bewegt, je nach Wahl waagerecht, senkrecht oder auf einem Kreis um den Koordinatenursprung.
Zusätzlich können Sie durch Markieren von Punktstrahlen, an diesen Punkt 24 Strahlen zeichnen lassen, deren Abbildung ebenso ermittelt wird.