„Bilder können nichts beweisen. Aber sie lassen Wissenschaftler die Funktion besser verstehen und vermitteln ihnen Ideen, wo sie mit neuen Überlegungen ansetzen können.“
Elias Wegert
 In der Mathematik versteht man unter der Niveaumenge die Menge aller Punkte eines Skalarfeldes, denen der gleiche Wert zugeordnet ist. Für zweidimensionale Skalarfelder ist diese Menge zumeist eine Linie und man spricht von einer Niveaulinie. Bei dreidimensionalen Skalarfeldern stellt diese Menge zumeist eine Fläche dar, die Niveaufläche genannt wird. Ein Beispiel für Niveauflächen sind die Äquipotentialflächen eines elektrischen Feldes.
In der Mathematik versteht man unter der Niveaumenge die Menge aller Punkte eines Skalarfeldes, denen der gleiche Wert zugeordnet ist. Für zweidimensionale Skalarfelder ist diese Menge zumeist eine Linie und man spricht von einer Niveaulinie. Bei dreidimensionalen Skalarfeldern stellt diese Menge zumeist eine Fläche dar, die Niveaufläche genannt wird. Ein Beispiel für Niveauflächen sind die Äquipotentialflächen eines elektrischen Feldes.
Niveauflächen können auch zur Veranschaulichung von Funktionen mehrerer reeller Veränderlicher bzw. komplexer Veränderlicher genutzt werden.
 Bei komplexwertigen Funktionen wird die Gaußsche Ebene zur Darstellung des Funktionsarguments genutzt und jeder Punkt durch eine Farbe gekennzeichnet, die entweder den Realwert, den Imaginärwert, den Betrag des Funktionswertes oder das Argument des Funktionswertes (Phasenplot) darstellt.
Bei komplexwertigen Funktionen wird die Gaußsche Ebene zur Darstellung des Funktionsarguments genutzt und jeder Punkt durch eine Farbe gekennzeichnet, die entweder den Realwert, den Imaginärwert, den Betrag des Funktionswertes oder das Argument des Funktionswertes (Phasenplot) darstellt.
Aus den entstehenden Darstellungen kann der Verlauf der Funktion (Täler, Berge, Unstetigkeitsstellen …) ermittelt werden.
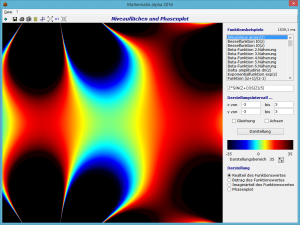
Abbildung rechts: Phasenplot f(z) = SIN(1/z5)+z
In diesem Programm können Sie diese Niveauflächen für komplexe Funktionen zeichnen.
Für die Funktionsgleichungen verwenden sie das Argument Z und folgende Funktionen und Operanden:
- Standardfunktionen SQRT, SIN, COS, TAN, COT, SEC, CSC, SINH, COSH, TANH, COTH, EXP, LN
- Spezielle Funktionen GAMMA und die Besselschen Funktionen BI0, BJ0
- Riemannsche Zetafunktion RIEMANN (Näherung bis … + 1/48z)
- die Jacobischen elliptischen Funktion DN, SN, CN
- Exponentialintegral EI
- die Funktionen TRE(Z) und TIM(Z) für den Real- bzw. Imaginärteil des komplexen Arguments z
- Operanden +, -, *, / und die Potenzbildung ^
- Konstanten I, PI
| Phasenplot, Niveauflächen |
|---|
 |
| Herunterladen |
Für die Zeichnung können Sie die Darstellungsintervalle sowohl in Abszissenrichtung (x-Achse) als auch in Ordinatenrichtung (y-Achse) eingeben.
Voreingestellt ist die Verwendung der im linken Fensterteil dargestellten Farben eines Regenbogens. Alternativ können Sie Farben verwenden, die im Maxwellschen Farbkreis auftreten.
Beachten Sie bitte, dass die aufwendige Berechnung und Darstellung auch auf schnellen Computern einige Zeit benötigt.
Complex Beauties
Die Idee zu diesem Teilprogramm stammt von den faszinierenden Mathematik-Kalendern „Complex Beauties“ von Prof. Elias Wegert der TU Bergakademie Freiberg. siehe https://blogs.hrz.tu-freiberg.de/mathekalender/
 Seit dem Jahr 2011 veröffentlichen Prof. Elias Wegert (Preisträger der XV.Internationalen Mathematikolympiade 1973 in Moskau) und Dr. Gunter Semmler vom Institut für Angewandte Analysis einen faszinierenden Mathematik-Kalender.
Seit dem Jahr 2011 veröffentlichen Prof. Elias Wegert (Preisträger der XV.Internationalen Mathematikolympiade 1973 in Moskau) und Dr. Gunter Semmler vom Institut für Angewandte Analysis einen faszinierenden Mathematik-Kalender.
Diese Kalender zeigen Visualisierungen komplexer Funktionen mit Hilfe sogenannter Phasenplots, d.h. „Komplexe Schönheiten“ (Complex Beauties).
Zu jedem Kalenderblatt gibt es gut geschriebene Erläuterungen der zu betrachtenden Bilder. Die Schönheit dieser mathematischen Darstellungen sollte man genießen. Eine Einführung in das Thema ist auf der Rückseite des Deckblattes enthalten.
In memoriam Wolfgang Ehrhardt
Leider ist Wolfgang Ehrhardt Anfang 2019 von uns gegangen.
Er schuf eine einzigartige Bibliothek von Pascal-Routinen, die schwierigste mathematische Verfahren hervorragend umsetzen und so vielen Programmierern Anregungen und Hilfestellungen gaben.
Die Langzahlarithmetik in „Mathematik alpha“ beruht auf seiner Leistung. Vielen Dank dafür.
| Phasenplot 2 |
|---|
 |
| Herunterladen |
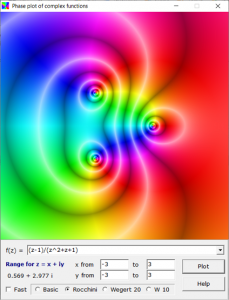
In Erinnerung an unsere Zusammenarbeit, bei der ich stets der Lernende war, stelle ich hier unser erweitertes Projekt „Phasenplot“ bereit. Ohne Wolfgang wäre es niemals gelungen, die Phasenplots nun auch mit Berücksichtigung der Beträge darzustellen.