Polyeder

In diesem Unterprogramm können Sie Polyeder – darunter alle Platonischen Körper – wählen. Nach Eingabe der entsprechenden Größen Kantenlänge, Höhe usw. ermittelt das Programm weitere Größen für die fünf regelmäßigen Körper, z.B.

• Volumen und Oberfläche
• Radius der Inkugel (diese Kugel berührt Flächenmittelpunkte)
• Radius der Mittelkugel (Kugel berührt Kantenmittelpunkte)
• Radius der Umkugel (Kugel berührt Körpereckpunkte)

Die Geschichte der regelmäßigen Körper ist bereits älter als unsere Zeitrechnung. Über Hippasos von Metapont (um 450 v.Z.) wird berichtet, dass er „… zuerst die aus 12 Fünfecken zusammengesetzte Kugel öffentlich beschrieb und deshalb als ein Gottloser im Meer umgekommen sei …“. Plato (429-348 v.Z.), nach dem sie benannt sind, ordnete diese fünf Körper in seinem Dialog „Timaios“ in Anlehnung an die Pythagoräer den Weltbestandteilen zu. Über Euklid (365-300 v.Z.) und Johannes Kepler (1571-1630) beschäftigen sich auch heute noch mathematisch Interessierte mit diesen Gebilden.
Beispiel: Für ein Ikosaeder mit der Kantenlänge a = 1 erhalten Sie:

Volumen	2.1817 RE
Oberfläche	8.6603 FE
Inkugelradius	0.7558
Mittelkugelradius	0.809
Umkugelradius	0.9511

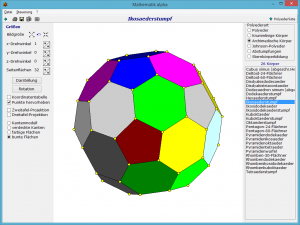
Zusätzlich zur Berechnung wird der gewählte Körper grafisch veranschaulicht. Voreingestellt ist ein Schrägbild mit Animationsmöglichkeit. Klicken Sie auf das Feld Zweitafelprojektion, erhalten Sie sowohl einen Aufriss als auch einen Grundriss. Haben Sie die Zweitafelprojektion markiert, so bewirkt das Feld Dreitafelprojektion zusätzlich die Darstellung eines dritten Risses, des Seitenrisses des Körpers.

Bei Auswahl eines anderen Körpers, z.B. eines Quaders, einer Pyramide, eines Pyramidenstumpfes usw., sind die unter Größen genannten Stücke einzugeben. In der Liste der Polyeder finden Sie neben konvexen auch zusammengesetzte Körper.

Archimedische Körper

Im dreidimensionalen Raum existieren genau fünf Körper, die ausschließlich von genau einer Art regelmäßiger Polygone begrenzt werden, den berühmten Platonischen Körpern, von Johannes Kepler auch Kosmische Körper genannt.
Schon Archimedes wusste, dass es weitere 13 sogenannte halbregelmäßige Körper gibt, die von mehr als einer Art regelmäßiger Vielecke begrenzt sind. Ihm zu Ehren nennt man diese Körpergruppe auch Archimedische Körper.

Archimedische Körper können aus den fünf Platonischen Körpern hergestellt werden. Dabei werden von den regelmäßigen Polyedern symmetrisch andere regelmäßige Körper abgeschnitten. Das Ikosidodekaeder entsteht zum Beispiel, indem an den Eckpunkten eines Pentagondodekaeders regelmäßige Tetraeder, also dreiseitige Pyramiden, entfernt werden. Während bei den Platonischen Körpern nur regelmäßige Dreiecke, Vierecke und Fünfecke als Seitenflächen vorkommen, können dies bei den Archimedischen Körpern nun auch Sechsecke, Achtecke und Zehnecke sein.

Anmerkung: Das abgestumpfte Ikosaeder ist der Archimedische Körper, welcher am besten eine Kugel annähert. Deshalb bildet dieses Polyeder die Grundlage für die Herstellung von Fußbällen usw.

Einige der Archimedischen Körper sind besonders interessant. Während die meisten der Körper eine Vielzahl von Symmetrieebenen aufweisen, fehlen diese beim Cubus simus und beim Dodecaedron simum (Bezeichnungen von Johannes Kepler). Beide zeichnen sich durch eine besonders hohe Anzahl von Dreiecksseitenflächen aus.
Dieses Teilprogramm bietet Ihnen die Möglichkeit, jeden der 13 Archimedischen Körper darzustellen und auf Wunsch wieder im Raum zu bewegen.

Außer den Platonischen und Archimedischen Körpern gibt es noch weitere interessante Körper, darunter zum Beispiel die zu den Archimedischen Körpern zählenden polaren Polyeder, die sogenannten Catalanschen Polyeder. Auch diese finden Sie in der Liste dieses Teilprogramms.

Johnson-Polyeder

Ein Polyeder heißt Platonischer Körper, wenn er nur von einer Art regelmäßiger N-Ecke begrenzt wird. Fordert man, dass an einer Ecke stets die gleiche Anzahl und Art von regelmäßigen N-Ecken zusammenstoßen und lässt verschiedene N-Ecke zu, so ergeben sich die Archimedischen Körper.
Begnügt man sich nun mit der Forderung nach regelmäßigen N-Ecken, verschiedener Eckenzahl und unterschiedlichen Polygonen an den Körperecken, so existieren weitere 92 derartige Körper. Erstmals wurden diese Polyeder von Johnson beschrieben und auch nach ihm benannt.

Im Programm können Sie alle 92 Körper betrachten. Auch hier ist es wieder möglich, ihre Anschaulichkeit durch Drehung zu erhöhen.

Darstellung und Animation der Körper

Die Darstellung der Körper kann verändert werden.
Ist die Darstellung des Körpers möglich, so können Sie ihn um seine räumliche Achsen bewegen und so die Anschaulichkeit verbessern.

Der Körper wird in einem räumlichen Koordinatensystem dargestellt. Starten Sie die Rotation, wird der Körper zur besseren Veranschaulichung um zwei Achsen gedreht. Mithilfe dieser Bewegung wird der räumliche Eindruck verstärkt sowie eine bessere Vorstellung der Gestalt des Körpers möglich.
Die Geschwindigkeit und Richtung der Drehung stellen Sie über die Pfeilschalter für die Drehung in x-, y- und z-Richtung ein.

An dieser Stelle sei noch auf die Berücksichtigung der Körperkanten hingewiesen. Diese können Sie, zumindest für die Polyeder, an dem Auswahlfeld verdeckte Kanten einstellen. Schalten Sie auf Kantenmodell, dann zeichnet das Programm ein Gittermodell des Körpers, d.h., alle Kanten werden sichtbar dargestellt.

Bei Beachtung der verdeckten Kanten stellt das Programm weiße Körperflächen dar. Auf Ihren Wunsch zeichnet das Programm auch farbige Seitenflächen. Zum einen werden bei bunte Flächen 24 Farben so verteilt, dass möglichst benachbarte Flächen unterschiedliche Färbungen besitzen. Markieren Sie das Feld farbige Flächen, so werden die Flächen in Abhängigkeit von ihrer Eckenzahl eingefärbt.

Die verwendeten Farben sind vordefiniert. Bei weißem Hintergrund werden Dreiecke gelb, Vierecke grün, Fünfecke rot, Sechsecke grau, Achtecke rosa und Zehnecke blau gezeichnet. Über die Schalter bis können Sie andere Farben für die Dreiecke, Vierecke … bis Zwölfecke auswählen.

2/3-Tafel-Projektion

Bei dieser Wahl stellt das Programm den gewählten Körper in Zweitafelprojektion (Grund- und Aufriss) bzw. Dreitafelprojektion dar. Auch hier können die Körper gedreht werden.

Polyederbibliothek

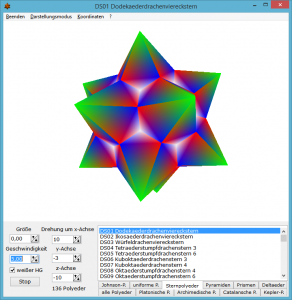In diesem Teilprogramm finden Sie eine Zusammenstellung von 2200 Polyedern verschiedener Art, d.h. dieser Programmteil enthält eine der weltweit, umfangreichsten Sammlungen von Polyedern.
Jedes Modell wird in Zentralperspektive dargestellt und um eine Achse gedreht.

Die darstellbaren Polyeder sind: Archimedische Körper, Archimedisch-Catalansche Hüllen, Catalansche Körper, selbstduale Dekaeder, Zehnflächner, Doppelkugel-Polyeder, selbstduale Dodekaeder, Zwölfflächner, Diamantpolyeder, dihedrale Rhomboeder, Drachenvierecksterne, facettierte Polyeder, Fast-Johnson-Polyeder, geodätische Kuppeln, isogonale und isohedrale Deltaeder, Cundy-Polyeder, koptische Polyeder, Ikosaedersterne, Johnson-Polyeder, duale Polyeder zu den Johnson-Polyedern, inverse Polyeder zu den Johnson-Polyedern, Kepler-Poinsot-Sternpolyeder, Keilkränze, Kronenpolyeder, krummlinig begrenzte Körper, Kuboktaedersterne, Coupoloïde, Molybi-Polyeder, Conway-modifizierte Polyeder, Platonische Körper, Doppelpyramiden, Petrie-Polyeder, Prismen bzw. Antiprismen, Polygramm-Prismen bzw. Antiprismen, abgestumpfte Prismen bzw. Antiprismen, Pyramiden, zirkuläre Prismen, Rhomboeder, Rhombendreißigflächnersterne, Zonoeder, Sphenoid-Prismen, Polyeder spezieller Symmetrie, Trapezoeder, selbstduale Tetradekaeder, Vierzehnflächner, Toroide, polyederische Tori, uniforme Polyeder, duale Polyeder zu den uniformen Polyedern, uniforme Verbundkörper, Verbundkörper, Akroeder, McNeill-Polyeder, spezielle abgestumpfte Körper, sonstige Polyeder und Körper

Polyederbibliothek
Herunterladen

Dieser Programmteil kann auch als einzelnes Programm geladen werden.

Beachten Sie bitte: Dieses Teilprogramm ist der einzige Programmteil, der eine zusätzliche Software verwendet, und zwar OpenGL. Sollte OpenGL nicht auf Ihrem Rechner installiert sein, kann dieses Teilprogramm leider nicht genutzt werden!