Ein pythagoreisches Tripel (auch: pythagoräisch) ist ein Tripel a,b,c von natürlichen Zahlen (verschieden von Null), welches die Gleichung erfüllt
a² + b² = c²
Sind u und v teilerfremde, ungerade natürliche Zahlen, so ist a,b,c ein derartiges Tripel mit
a = u · v , b = (u² – v²)/2 , c = (u² + v²)/2
Diese Lösungsmethode wurde schon von den Chinesen der Han-Periode (ungefähr 200 v.u.Z. – 200 u.Z.) benutzt. Aber auch schon Diophant von Alexandria war eine Lösungsmethode bekannt. Für ein gerades x = 2pq setzte er
z+y = 2p² ; z – y = 2q² ; z = p² + q² ; y = p² – q²
Vor Diophant besaßen auch die Babylonier der Hammurabi-Dynastie eine eigene Lösungsmethode zur einfachen Berechnung pythagoreischer Zahlentripel. Schließlich fand man ähnliche Berechnungen auch in Hindu Texten über die Konstruktion von Altären aus der Zeit von 500 – 200 v.u.Z. Nach van der Waerden ist es sehr wahrscheinlich, dass die ganze Theorie einen gemeinsamen Ursprung hat. Er vermutet, dass der berühmte Lehrsatz vor der Hammurabi-Periode von einem mathematisch gebildeten Priester entdeckt wurde.
Kleinste Zahlentripel
Tripel, die keinen gemeinsamen Teiler besitzen, wie z.B. 6,8,10, werden primitive Tripel genannt. Die kleinsten primitiven Tripel sind
| 3,4,5 | 5,12,13 | 8,15,17 | 7,24,25 |
| 20,21,29 | 12,35,37 | 9,40,41 | 28,45,53 |
| 16,63,65 | 11,60,61 | 33,56,65 | 48,55,73 |
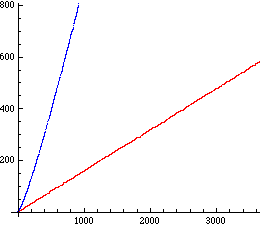 In der Grafik ist das Wachstum der Anzahl primitiver Tripel bis zu einer maximalen Größe der Hypotenuse rot eingezeichnet. Die blaue Kurve gibt die Häufigkeit aller pythagoreischer Tripel an.
In der Grafik ist das Wachstum der Anzahl primitiver Tripel bis zu einer maximalen Größe der Hypotenuse rot eingezeichnet. Die blaue Kurve gibt die Häufigkeit aller pythagoreischer Tripel an.
Das Wachstum primitiver Tripel ist linear. Für die Anzahl n primitiver Tripel bis zu einer Grenze g (g < größte Zahl des Tripels) gilt genähert:
n ≈ (ln 2)/π² · g = 0,07023 g
Neben dem 3-4-5-Dreieck gibt es noch mindestens ein anderes, dessen Fläche sich mit Hilfe einer einzigen Ziffer ausdrücken lässt: 693-1924-2045, dessen Fläche 666 666 ist. Weitere derartige Tripel wurden unter 1040 noch nicht gefunden.
Ein Sechstel der Flächeninhalte aller pythagoreischen Dreiecke endet mit der 6, ein weiteres Sechstel endet auf 4, die restlichen 2/3 besitzen einen Inhalt, der auf 0 endet.
Es gibt unendlich viele rechtwinklige Dreiecke mit der Eigenschaft, dass sich die Längen von Hypotenuse und einer Kathete um genau eins unterscheiden. (3²+4²=5² / 5²+12²=13² …) Es gibt auch unendlich viele, deren Katheten um eins differieren. Allerdings existiert nur genau ein Tripel dreier aufeinanderfolgender natürlicher Zahlen, natürlich 3-4-5.
Tripel-Berechnung
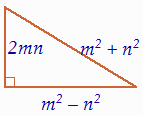 Ausgehend von der Beziehung
Ausgehend von der Beziehung
(m² – n²)² + (2mn)² = (m² + n²)²
können ebenso pythagoreische Tripel erzeugt werden. Sind m und n verschiedene natürliche Zahlen mit m > n, so erhält man mit
a = m² – n² ; b = 2mn ; c = m² + n²
ein solches Tripel. In der englischsprachigen Literatur wird das Verfahren als m-n-Formel bezeichnet.
Dieses Verfahren erzeugt nicht nur primitive pythagoreische Tripel. Diese werden alle(!) erzeugt, für nichtprimitive Tripel gilt dies nicht.
Für m = 2, n = 1 erhält man das Tripel (3, 4, 5). Das Tripel (9, 12, 15) ist dagegen durch keine Wahl von m und n konstruierbar.
Zwei-Brüche-Verfahren
Außer dem pythagoreischen und babylonischen Verfahren gibt es weitere Methoden, pythagoreische Zahlentripel zu erzeugen.
Bei dem Zwei-Brüche-Verfahren wird von zwei rationalen Zahlen a/b und c/d ausgegangen, deren Produkt 2 sein muss. Dabei dürfen b und d gleich 1 sein, d.h. natürliche Zahlen liegen vor.
1) jeder der Brüche wird um 2 vergrößert
2) die Brüche werden über Kreuz miteinander multipliziert, d.h. Nenner und Zähler des jeweils anderen Bruchs. Im Ergebnis entstehen zwei natürliche Zahlen des Tripels.
3) um die 3.Zahl zu finden, werden beide Zahlen quadriert, addiert und die Wurzel gezogen
Zum Beispiel wird für a/b = 4/2 und c/d = 2/2
1) (8/2 und 6/2 ; 2) 16 und 12 ; 3) 16²+12² = 400, d.h. 3.Zahl = 20
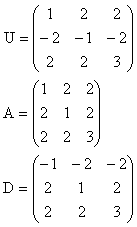 Ist (a0, b0, c0) ein pythagoreisches Zahlentripel, so erhält man durch
Ist (a0, b0, c0) ein pythagoreisches Zahlentripel, so erhält man durch
(a1 , b1, c1) = (a0, b0, c0) U
(a2 , b2, c2) = (a0, b0, c0) A
(a3 , b3, c3) = (a0, b0, c0) D
weitere pythagoreische Tripel.
Sind a0 und b0 zueinander teilerfremd, so nennt man das Tripel (a0, b0, c0) reduziert bzw. primitiv.
1977 bewies Roberts, dass ein pythagoreisches Tripel genau dann primitiv ist, wenn es in der Form (3, 4, 5) · M geschrieben werden kann, wobei die Matrix M ein endliches Produkt der drei abgebildeten Matrizen A, D bzw. U ist.
Für alle pythagoreische Tripel gilt weiterhin
– das Produkt der Kathetenlängen (d.h. der zwei kleineren Zahlen) ist durch 12 teilbar
– das Produkt aller drei Tripelzahlen ist durch 60 teilbar
– die Summe der drei Zahlen ist Teiler ihres Produktes
Bis heute ist nicht bekannt, ob zwei verschiedene Tripel das gleiche Produkt haben.
Die ersten Tripel, bei denen zwei Zahlen sich nur um 1 unterscheiden, sind nach aufsteigendem c geordnet: (3, 4, 5), (5, 12, 13), (7, 24, 25), (20, 21, 29), (9, 40, 41), (11, 60, 61), (13, 84, 85), (15, 112, 113), …
Die ersten 16 primitiven Tripel (geordnet nach c) sind: (3, 4, 5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (33, 56, 65), (16, 63, 65), (48, 55, 73), (36, 77, 85), (13, 84, 85), (39, 80, 89), (65, 72, 97), … Zu diesen gehören die Inkreisradien 1, 2, 3, 3, 6, 5, 4, 10, 5, …