 1796 bewies Carl Friedrich Gauß, dass sich das regelmäßige Siebzehneck allein mit Zirkel und Lineal konstruieren lässt.
1796 bewies Carl Friedrich Gauß, dass sich das regelmäßige Siebzehneck allein mit Zirkel und Lineal konstruieren lässt.
Satz von Gauß: Es sind ausschließlich diejenigen regelmäßigen N-Ecke mit Zirkel und Lineal konstruierbar, deren ungerade Eckenzahl n ein Produkt Fermatscher Primzahlen
f = 22^k + 1
(alle in 1.Potenz) ist. Bekannt sind die Fermatschen Primzahlen f = 3, 5, 17, 257, 65537.
Euklid gelang es schon N-Ecke mit n = 3, 4, 5, 6, 8, 10, 12, 16, 20, 24, 32, 48 und 64 zu konstruieren. Dass die obige Bedingung hinreichend ist, konnte der 19jährige Gauß im Jahre 1796 nachweisen. Die Notwendigkeit der Beziehung bewies 1836 Wantzel.
Für genau 24 Zahlen n unter 100 lässt sich ein n-Eck konstruieren: 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96.
Das regelmäßige Siebzehneck ist ein Vieleck mit 17 Ecken, 17 gleich langen Seiten, 17 gleich großen Innenwinkeln von 158 14/17°.
Ist die Seite a gegeben, so können Inkreisradius r und Umkreisradius R, die Diagonalen d2 bis d8, Höhe h, Flächeninhalt A und Umfang u berechnet werden. Da das regelmäßige Siebzehneck mit Zirkel und Lineal konstruierbar ist, existieren exakte Gleichungen, die allerdings sehr umfangreich sind.
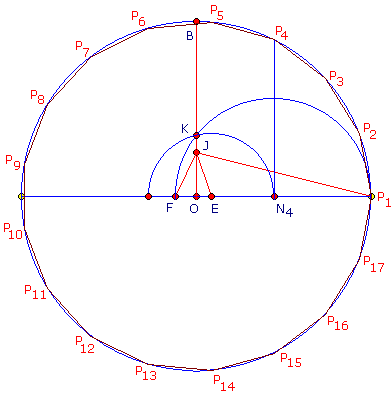 Konstruktionsbeschreibung:
Konstruktionsbeschreibung:
Gegeben ist ein Punkt O.
1. Zeichnen eines Kreises um O und eines Durchmessers durch O
2. rechter Schnittpunkt des Durchmessers und des Kreises ist P1
3. Konstruktion der Senkrechten zu OP1, Schnittpunkt ist B
4. Konstruktion von J mit 4 OJ = OB
5. Verbinden von J und P1, Ermitteln von E, so dass der Winkel ∠ OJE ein Viertel des Winkels ∠ OJP1 ist
6. Konstruktion von F, so dass Winkel ∠ EJF gleich 45° ist
7. Konstruktion des Halbkreises über FP1, dieser schneidet OB in K
8. Zeichnen eines Halbkreises um E mit dem Radius EK, dieser schneidet OP1 in N4
9. die Senkrechte in N4 schneidet den Ausgangskreis in P4
10. ausgehend von P1 und P4 ergeben sich durch Abtragen deren Entfernung auf dem Kreis die Punkte P7, P10, P13, P16, und im zweiten bzw. dritten Umlauf die restlichen Punkte des regelmäßigen 17-Ecks.
Das Ergebnis kann mit dem Teilprogramm Planimetrie / Konstruktionen kontrolliert werden. Dazu wird in der aufklappbaren Liste der Eintrag Regelmäßiges 17-Eck ausgewählt.
Analytische Herleitung
Die Eckpunkte des Siebzehnecks erfüllen die komplexe Gleichung
z17 = 1
Eine Lösung ist z = 1. Die anderen Eckpunkte ergeben sich aus
(z17 – 1)/(z – 1) = z16 + z15 + … + z³ + z² + z + 1 = 0
a sei eine Wurzel der Gleichung. Da die Restklassengruppe Z17 zyklisch erzeugt werden kann, ist der Ansatz z0 = a ; z1 = a3 ; z2 = a9 ; z3 = a27 = a10 ; z4 = a13 ; z5 = a5 ; z6 = a15 ; z7 = a11 ; z8 = a16 ; z9 = a14 ; z10 = a8 ; z11 = a7 ; z12 = a4 ; z13 = a12 ; z14 = a² ; z15 = a6 möglich.
Ansatz:
X = z0 + z2 + z4 + z6 + z8 + z10 + z12 + z14
x = z1 + z3 + z5 + z7 + z9 + z11 + z13 + z15
Da die zi alle Potenzen von a1 bis a16 darstellen, wird X + x = -1. Das Produkt Xx ergibt nach Ausmultiplizieren viermal jede der Potenzen, d.h. Xx = -4. X und x sind damit Lösungen der quadratischen Gleichung t²+t-4 = 0 mit X = (-1 + √17)/2 und x = (-1 – √17)/2.
Ansatz:
U = z0 + z4 + z8 + z12 ; u = z2 + z6 + z10 + z14
V = z1 + z5 + z9 + z13 ; v = z3 + z7 + z11 + z15
mit U + u = X, V + v = x, Uu = -1 und Vv = -1 sowie den quadratischen Gleichungen t²-Xt-1 = 0 bzw. t²-xt-1 = 0 und den Lösungen
U = (X + √(X² +4))/2 ; V = (x + √(x² + 4))/2
u = (X – √(X² + 4))/2 ; v = (x – √(x² + 4))/2
Ansatz:
W = z0 + z8 = a + a16 und w = z4 + z12 = a13 + a4
mit W + w = U und Ww = V, d.h. t² – Ut + V = 0 und den Lösungen
W = (U + √(U² – 4V))/2 ; w = (U – √(U² – 4V))/2
Konstruktionsbeschreibung
1) X und x konstruieren
2) U und V konstruieren
3) W konstruieren
4) da a und a16 den gleichen Realteil besitzen, hat der Mittelpunkt von OW den gleichen Realteil wie a bzw. a16
Realteil von
a = √(- √((19 √17 + 85)/2048) + (3 √17 + 17)/64)+ √((17 – √17)/128) + √17/16 – 1/16 = 0,932472…
5) die restlichen Eckpunkte des Siebzehnecks sind durch Streckenabtragen konstruierbar.
Regelmäßiges Fünfeck
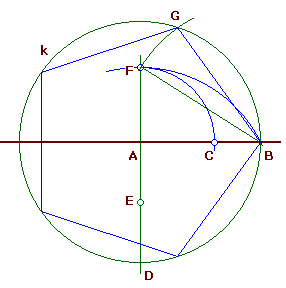 Aufgabe: Ein regelmäßiges Fünfeck ist in einen Kreis mit dem Radius AB einzubeschreiben.
Aufgabe: Ein regelmäßiges Fünfeck ist in einen Kreis mit dem Radius AB einzubeschreiben.
Lösung:
Ohne Beschränkung der Allgemeinheit sei AB = 1. Dann ergibt sich für die Strecke
AC = x1,2 = (-1 ± √5)/2
Die positive Lösung φ = (√5 – 1)/2 ist die Verhältniszahl des goldenen Schnitts.
Konstruktion:
1. Um A wird ein Kreis mit dem Radius AB gezogen.
2. Punkt D wird so gewählt, dass der Winkel DAB = 90° ist.
3. E ist der Mittelpunkt der Strecke AD
4. Um E wird ein Kreis mit dem Radius EB gezeichnet.
5. Dieser Kreis schneidet die Gerade AD im Punkt F.
6. BF ist die Seitenlänge des regelmäßigen Fünfecks, AF die Seitenlänge des regelmäßigen Zehnecks, welche dem Ausgangskreis um A einbeschrieben sind.
Anmerkung: Der Schnittpunkt des Kreises um A mit Radius AF schneidet dann die Strecke AB im Punkt C. Dieser teilt AB stetig.
Regelmäßiges 257-Eck
Eine analytische Herleitung der Konstruktion des regelmäßigen 257-Ecks finden Sie im nachfolgenden Text:
Regelmäßiges 65537-Eck
Eine Beschreibung der Konstruktionsberechnung des regelmäßigen 65537-Ecks finden Sie im nachfolgenden Text, die von Ken Brakke (brakke@susqu.edu) ermittelt wurde. Das Programm berechnet die im Text genannten Hilfsgrößen.