Gleichdicke, z.B. Reuleaux-Räder, sind zylindrische Hohlkörper, deren Leitkurve aus Kreisbögen zusammengesetzt ist. Die längste Sehne von einem Punkt der Leitkurve zu einem anderen ist stets gleich lang.
Derartige Figuren wurden erstmals 1778 von Euler untersucht. Intensive Studien lieferte 1875 Franz Reuleaux (1829-1905).
Das Standard-Gleichdick ist das Kreisbogendreieck oder Reuleaux-Dreieck. Die Figur besteht aus einem gleichseitigen Dreieck mit drei auf die Seiten gesetzten Kreisabschnitten. Man erhält die Kreisbögen, in dem man um jeden Dreieckseckpunkt einen Kreisbogen mit dem Radius der Dreiecksseite zeichnet.
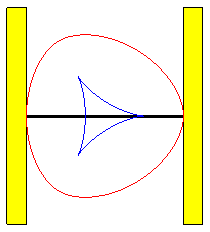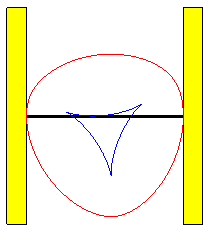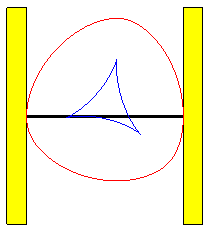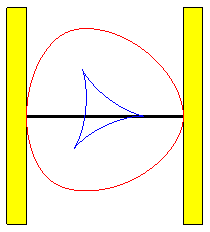Das Besondere an Reuleaux-Dreiecken ist, dass diese als Räder eines Fahrzeuges verwendet werden können. Dabei ist der Abstand zwischen unterstem und obersten Punkt der Dreiecke konstant.
Die spezielle Rolleigenschaft sieht man auch in der Darstellung.
| Reuleaux-Räder |
|---|
|
| Herunterladen |
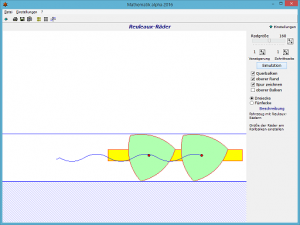
Im Programm Reauleaux-Räder wird ein solches Fahrzeug demonstriert.
Eingestellt werden kann, ob Reuleaux-Dreiecke oder -Fünfecke genutzt werden sollen; außerdem die Radgröße.
Während der Simulation wird das Fahrzeug kontinuierlich von links nach rechts bewegt.
Auch wenn solche Räder möglich sind, erkennt man, dass Fahrgäste ziemlich durchgeschüttelt würden.