 Nach der berühmten Riemannschen Vermutung liegen alle nicht trivialen Nullstellen der Zetafunktion ζ(z) in der Gaußschen Zahlenebene auf einer Geraden mit dem Realteil 0,5.
Nach der berühmten Riemannschen Vermutung liegen alle nicht trivialen Nullstellen der Zetafunktion ζ(z) in der Gaußschen Zahlenebene auf einer Geraden mit dem Realteil 0,5.
Zur Veranschaulichung zeichnet das Programm die Riemannsche Zetafunktion für Argumente 0,5 + i t, wobei t eine reelle Zahl ist.
In der ebenen Darstellung werden Real- und Imaginärteil als rote und blaue Kurve einzeln angetragen. Die Stellen, an denen beide Kurven sich auf der Abszissenachse schneiden, sind die berühmten, nicht trivialen Nullstellen der Zetafunktion.
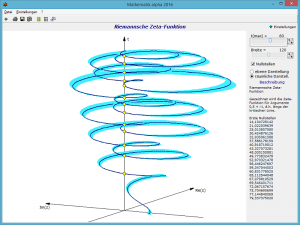
In der räumlichen Darstellung wird der Wert für t nach oben angetragen, die Funktionswerte in Real- und Imaginärteil getrennt in der Gaußschen Zahlenebene.
Dabei entsteht eine sich um die t-Achse (Realteil 0,5) windende Kurve, die immer dann die Achse schneidet, wenn eine Nullstelle vorliegt.
| Riemannsche Zeta-Funktion |
|---|
 |
| Herunterladen |
Markieren Sie das Feld Nullstellen, so werden die im Darstellungsbereich vorhandenen Nullstellen angezeigt.
Die ersten Nullstellen sind: 14,134725142 ; 21,022039639 ; 25,010857580 ; 30,424876126 ; 32,935061588 ; 37,586178159 ; 40,918719012 ; 43,327073281 ; 48,005150881 ; 49,773832478 ; 52,970321478 ; 56,446247697 ; 59,347044003 ; 60,831778525 ; …