 Dieses Puzzle wurde erstmals 1878 von Sam Loyd beschrieben und wird daher auch Loyd’s 15 genannt.
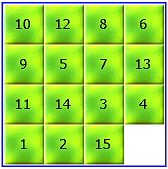
Dieses Puzzle wurde erstmals 1878 von Sam Loyd beschrieben und wird daher auch Loyd’s 15 genannt.
Es besteht aus 15 Quadraten, welche die Ziffern 1 bis 15 enthalten, die in einem 4 x 4-Quadrat angeordnet sind. Das 16. Feld bleibt frei.
Aufgabe ist es, die 15 zunächst unsortierten Quadrate durch Verschieben jeweils eines Quadrats auf die leere Position numerisch zeilenweise von links nach rechts zu ordnen.
Je nach Ausgangssituation ist dies in endlich vielen Schritten möglich oder prinzipiell unmöglich.
Wird die Summe S der Anzahl von Quadraten i (i = 1, 2, …, 15) gebildet, die sich auf einer von links oben zeilenweise nach rechts unten gezählten richtigen Position i befinden, mit i < 15, so kann das Puzzle genau dann korrekt geordnet werden, wenn S gerade ist.
Betrachtet man ein entgegengesetzt angeordnetes 3 x 3-Puzzle mit den Zahlen 1 bis 8, so ist von diesem bekannt, dass es auf zehn verschiedene Arten in mindestens 30 Zügen geordnet werden kann. Für 32 Züge gibt es schon 112 Möglichkeiten, für 34 Züge 512.
In diesem Teilprogramm können Sie dieses Puzzle testen. Klicken Sie auf eine Zahl, die an das leere Feld angrenzt, so wird dieses Quadrat verschoben.
Die Größe des Puzzles können Sie von 3 x 3 bis 8 x 8 Felder einstellen.
Beachten Sie aber, dass die Lösung des 8 x 8-Puzzles durchaus mehr als eine Stunde Zeit benötigt.
Download
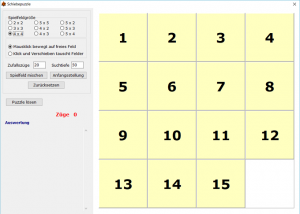
| Spiel 15 (Loyds Puzzle) |
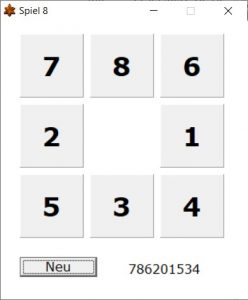
Spiel 8 |
|---|---|
 |
 |
| Herunterladen | Herunterladen |
Dieses Spiel steht hier zum Download bereit; die Variante ermöglicht die Berechnung eines Lösungswegs für verschiedene Puzzle-Größen und Anfangssituationen.
Das „Spiel 8“ ist eine stark vereinfachte Variante. Der ZIP-Datei sind die Delphi-Quelltexte hinzugefügt. Diese Lösung kann als Beispiellösung für den Informatik-Unterricht genutzt werden.