 Besonders schöne Fraktale erhalten Sie in den Teilprogrammen Apfelmännchen, Julia-Mengen und deren Verbindung miteinander unter Mandelbrot-Julia-Mengen.
Besonders schöne Fraktale erhalten Sie in den Teilprogrammen Apfelmännchen, Julia-Mengen und deren Verbindung miteinander unter Mandelbrot-Julia-Mengen.
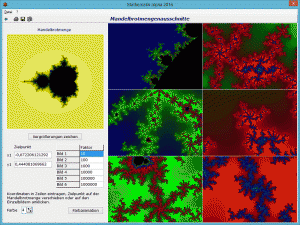
In diesem Programm können Sie an der Mandelbrotmenge z² + c, dem Apfelmännchen, Vergrößerungen zeichnen lassen.
In der links dargestellten Mandelbrotmenge befindet sich ein roter Punkt. Dieser beschreibt die Koordinaten des Mittelpunktes aller zu zeichnenden Vergrößerungen. Diesen Punkt können Sie mit der Maus verschieben oder in die Eingabefelder Zielpunkt dessen Koordinaten direkt eintragen.
Wählen Sie Vergrößerungen zeichnen, so konstruiert das Programm sechs Ausschnitte der Mandelbrotmenge.
Die zugehörigen Vergrößerungsfaktoren können in der Tabelle verändert werden. Der größtmögliche Faktor ist 100 Millionen!
Beachten Sie bitte: Die sehr komplexen Berechnungen und Darstellungen erfordern auch auf schnellen Computern einige Zeit. Unter Umständen kann dies sogar sehr lange dauern, insbesondere wenn Sie einen Zielpunkt gewählt haben, der sich in einem Konvergenzbereich befindet. Abbrechen können Sie mit dem entsprechenden Schalter.
| Mandelbrotmenge | |
|---|---|
 |
|
| Herunterladen | |
Erklärung der Mandelbrotmenge
Die Mandelbrotmenge ist die Menge aller komplexen Zahlen c, für welche die durch
z0 = 0 ; zn+1 = zn² + c
rekursiv definierte Folge beschränkt ist. Bilder der Mandelbrotmenge können erzeugt werden, indem für jeden Wert des Parameters c ein Farbwert in der komplexen Ebene zugeordnet wird.
Die grafische Darstellung wurde später von der Bremer Forschungsgruppe für komplexe Dynamik Apfelmännchen genannt.
Entstehung der Mandelbrotmenge
Die Berechnungsformel der Mandelbrotmenge lautet vereinfacht „quadriere die Zahl z und addiere die Zahl c“. Da z eine komplexe Zahl ist, kann das Ergebnis in der Gaußschen Zahlenebene veranschaulicht werden.
Eine komplexe Zahl besteht aus zwei Teilen (bzw. Zahlen) und kann daher einen Punkt in der zweidimensionalen komplexen Ebene darstellen. Die Berechnungsformel wird benutzt, herauszufinden, welche Farbe solch ein Punkt bekommen soll.
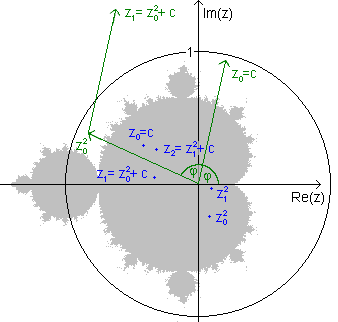 Die Abbildung zeigt den ersten Iterationsschritt zweier Punkte (grün und blau): Der Punkt z0 (rechter grüner Pfeil) dessen Farbe bestimmt werden soll, wird zunächst quadriert. Das Ergebnis ist der Punkt, auf den der mittlere grüne Pfeil zeigt. Nun wird der Startpunkt c addiert und man z1 (ganz oben).
Die Abbildung zeigt den ersten Iterationsschritt zweier Punkte (grün und blau): Der Punkt z0 (rechter grüner Pfeil) dessen Farbe bestimmt werden soll, wird zunächst quadriert. Das Ergebnis ist der Punkt, auf den der mittlere grüne Pfeil zeigt. Nun wird der Startpunkt c addiert und man z1 (ganz oben).
Für weitere Schritte wird der Punkt in die Gleichung
zn+1 = zn² + c
eingesetzt. Das Ergebnis zn+1 wird solange immer wieder neu als zn genutzt, bis der Abstand des berechneten Punktes vom Ursprung einen bestimmten Wert (z.B. 100) überschreitet:
z0 = c ; z1 = z0² + c ; z2 = z1² + c ; …
Ist der Abstand von zn zum Ursprung auch nach einer festgelegten Anzahl von Iterationen immer noch klein, so konvergiert die Zahlenfolge und dieser Punkt wird in der Regel schwarz eingefärbt. Wird der Abstand von 100 jedoch schon bei der n-ten Iteration überschritten, so wird die n-te Farbe einer Farbpalette ausgewählt.
Beziehung Mandelbrotmenge-Juliamengen
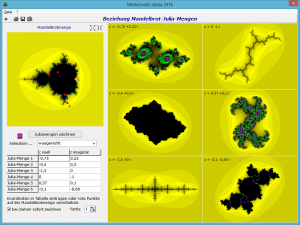 Mit dem Apfelmännchen sind weitere Fraktale verwandt: die sogenannten Juliamengen.
Mit dem Apfelmännchen sind weitere Fraktale verwandt: die sogenannten Juliamengen.
Die Berechnung einer Juliamenge unterscheidet sich nur in der Addition der Konstanten c. Während beim Apfelmännchen für jeden zu berechnenden Bildpunkt eine andere Konstante verwendet wird, nämlich die komplexe Koordinate des zu berechnenden Punktes, ist die Konstante c bei der Juliamenge für jeden Punkt gleich. D.h.:
- z0 ist weiterhin der Punkt, dessen Farbe bestimmt werden soll,
- c ist jedoch unabhängig von dem zu berechnenden Punkt.
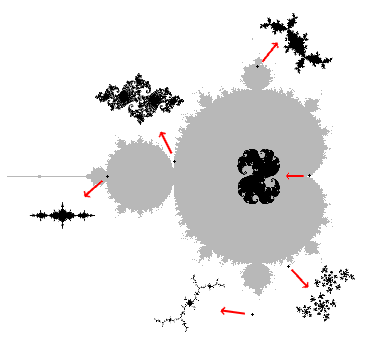 Durch Variation der Konstanten c kann sehr unterschiedliche Juliamengen erhalten. Dabei gilt:
Durch Variation der Konstanten c kann sehr unterschiedliche Juliamengen erhalten. Dabei gilt:
- wird der Wert aus dem schwarzen Bereich des Apfelmännchens gewählt, so entstehen zusammenhängende Gebilde.
- wird ein Wert außerhalb gewählt, entstehen mehrere nicht miteinander verbundene Gebilde.
Die interessantesten Formen entstehen, wenn man c aus dem Rand des Apfelmännchens wählt.
Faszinierend ist der Übergang an der Grenze des schwarzen Bereichs: Während zuerst ein zusammenhängendes Gebiet zu sehen ist, löst sich dieses immer mehr auf, bis schließlich getrennte Bereiche zu erkennen sind.
Diese Beziehung zwischen der Mandelbrotmenge und den zugehörigen Juliamengen kann in diesem Teilprogramm untersucht werden.
In der links dargestellten Mandelbrotmenge sind sechs rote Punkte eingezeichnet. Diese beschreiben die Koordinaten von sechs entsprechenden Juliamengen. Die Punkte können mit der Maus verschoben werden. Außerdem können Sie die Koordinaten auch direkt in die Tabelle eintragen.
Wählen Sie Juliamengen zeichnen, so zeichnet das Programm die sechs Juliamengen.
Beachten Sie bitte: Die sehr komplexe Berechnung erfordert auch auf schnellen Computern einige Zeit.
Animation der Juliamengen
Verschieben Sie einen der Punkte in der Mandelbrotmenge und haben Sie das Feld bei Ziehen sofort zeichnen markiert, so können Sie die Änderung unmittelbar nachvollziehen.
Auch diese Darstellung erfordert die volle Leistung Ihres Prozessors. Auf etwas langsameren Computern kann es daher zu einer ruckartigen Bewegung kommen.
| Juliamengen am Apfelmännchen |
|---|
 |
| Herunterladen |
Punkt 1 kann zusätzlich automatisch verschoben werden. Diese Animation starten und stoppen Sie über den Schalter.
An der aufklappbaren Liste können Sie wählen, wie Punkt 1 bewegt wird. Insbesondere die oben beschriebene Bewegung auf der Kardioide des Apfelmännchens ist sehr interessant.
