Zahlenlexikon

„Es ist genau so, als frage man, warum Beethovens Neunte so schön ist. Wenn Sie nicht sehen warum, dann kann es ihnen auch niemand erklären. Ich weiß, dass Zahlen wunderschön sind.
Wenn Sie es nicht sind, dann ist nichts schön.“
Paul Erdös

Die Zahl ist ein grundlegender Begriff der Mathematik.
Der abstrakte Zahlenbegriff ist das Ergebnis eines Jahrtausende langen Entwicklungsprozesses.
Die natürlichen Zahlen entstanden aus dem praktischen Bedürfnis, Gegenstände zu zählen. Sie bedeuten Anzahlen von Gegenständen, die zum Zählen in geeigneter Weise angeordnet und mit den Elementen einer bekannten anderen Menge verglichen wurden.
Das Zählen gehörte bereits zu den Bedürfnissen der Menschen auf einer sehr frühen Entwicklungsstufe. Die Zahlen, mit denen man zählen und abzählen kann, d.h. die Zahlen 1, 2, 3, 4, 5, 6, 7, … sind folglich sehr alt.
Deshalb gehören Zahlwörter zu den ältesten Bestandteilen der Sprachen. Diese Zahlen im ursprünglichen Sinne, die sich ganz natürlich ergeben, sind die natürlichen Zahlen.

Auf den nachfolgenden Seiten werden interessante und merkwürdige Eigenschaften dieser natürlichen Zahlen vorgestellt.

Zahl 0

„In der Kulturgeschichte wird die Entdeckung der Null immer als eine der größten Leistungen der Menschheit herausragen“
Tobias Danzig, „Number, The language of science“

Die Ziffer 0 ermöglicht unser Stellenwertsystem.
Im Laufe der Geschichte wurde die Zahl Null dreimal erfunden: von den Babyloniern, den Mayas und zuletzt von den Indern.

Schon 200 v.u.Z. verwendeten indische Mathematiker für die Null einen Punkt als Leerzeichen. Dieses Zeichen wurde „shunya“ genannt und bedeutete „nichts“.
Im 5.Jahrhundert wurde in Indien für jede dezimale Stelle dieselbe Menge von 9 Ziffern verwendet. Dazu war es notwendig, für fehlende Werte auf einer bestimmten Zehnerpotenz ein neues Symbol zu verwenden, eine zehnte Ziffer, die Null.
Aryabhata benutzte um 500 ein positionales Zahlsystem ohne Null, jedoch für die Null das Wort „kha“.

Allgemein wird als erster gesicherter Beweis der Null als Zahl in Indien eine Steintafel aus dem Ort Gwalior 500 km südlich von Neu-Delhi mit den Daten 27.Dezember 786, 10.Januar 787 und 17.Januar 787 angesehen, die von einer Gartenanlage handelt, dessen Länge 270 (hastas) beträgt und 50 Blumengirlanden erhielt.

Die früheste, schriftlich nachweisbare Verwendung der Null findet sich in der Inschrift K.151 in dem Tempel Sambor Prei Kuk (Abbildung) in Kambodscha vom Anfang des 7.Jahrhunderts und berichtet von der Errichtung einer Götterstatue am 14. April 598.
Das hier benutzte Jahr der Saka-Ära ist 520, wobei die Null mit dem Begriff kha (Luftraum) wiedergegeben ist.
Der Tempel Sambor Prei Kuk befindet sich in der alten Stadt Isanapura. Sie wurde 615-625 von Isanavarman I. erbaut.
Isanapura war die Hauptstadt des Königreiches von Chenla, das hier im siebenten und achten Jahrhundert blühte. Die Ruinen bestehen aus über 150 Tempel und Türmen und bedecken ein Gebiet von über 300 Hektar. Es gibt drei Hauptkomplexe, die von Mauern umgeben waren. Die Tempelbauten sind reich mit Reliefs dekoriert.

Im 9.Jahrhundert lernten arabische Mathematiker die Null kennen und bezeichneten sie mit „sifr“, was wörtlich übersetzt „leer“ bedeutet.
Aus „sifr“ entwickelte sich das Wort „Ziffer“. Fibonacci nannte im 12.Jahrhundert die Null italienisch „zefiro“, kurz „zero“, was ebenfalls „leer“ kennzeichnet. In Latein entspricht dies „nullus“.

In Europa tat man sich schwer mit einer Zahl die gar keine Zahl ist, sondern das Nichts beziffert, gleichzeitig aber jede vor ihr stehende Zahl verzehnfacht. Es dauerte lange bis die Rechenlehrer der frühen Neuzeit dem Volk den hohen Wert dieser „wertlosen“ Zahl nahe bringen konnten.
Europa teilt sich heute in eine zero-Region und eine nullus-Region.

Zero oder eine einfache Veränderung wird im Englischen (zero), Catalanischen, Französischen (zéro), Portugiesischen (zero), Rumänischen (zero), Spanischen (cero), Wallonischen (zérô), Albanischen, Polnischen (zero), Japanischen, usw… verwendet.
Die nullus-Region besteht aus den deutschsprachigen Ländern, Skandinavien und einigen Ländern mit slawischer Sprache, z.B. Latein (nullus), Bulgarisch (nula), Dänisch (nul), Finnisch (nolla), Niederländisch (nul), Isländisch (núll), Tschechisch (nula), Russisch (nul), Schwedisch (noll), Slowakisch (nula) …
Im Griechischen wird u.a. mhden genutzt, was ursprünglich „nichts“ darstellte.

Auch im 21.Jahrhundert wird die Null noch immer von der Mehrzahl der Menschen als unnatürlich angesehen. Dabei ist das Zählen mit Null ist unserer Kultur nicht fremd.

Der Gedanke, den ersten Tag des Monats als den Tag Null zu bezeichnen, wäre ungewöhnlich. Allerdings wird dieses Prinzip bei den Stunden eines Tages tatsächlich angewendet wird:
Ruft man um Mitternacht die Zeitansage an, so hört man nämlich tatsächlich „Beim nächsten Ton des Zeitzeichens ist es: null Uhr, null Minuten und zehn Sekunden.“ Die Stunden-, Minuten und Sekundenzählung beginnt bei Null und vereinfacht so auch viele Rechnungen.

Bei Bläsern und teilweise Gitarristen ist im Fingersatz der Daumen „0“, der Zeigefinger „1“ usw. Damit ist das Beginnen mit Null selbst beim Abzählen der Finger unserer Kultur nicht ganz fremd. Bei Saiteninstrumenten bezeichnet die „0“ auch eine nichtgegriffene Saite.

Manchmal wird die Auffassung vertreten, die Null sei ja gar keine „richtige Zahl“. Solche Auffassungen hängen von der Kultur ab, in der man lebt. Tatsächlich war für die alten Griechen die Eins keine Zahl, sondern die Einheit, aus der alle Zahlen konstruiert werden konnten. Es ist also nur eine Gewohnheitssache.

Mathematische Eigenschaften:
Die Null ist das neutrale Element der Addition im Primring der ganzen Zahlen sowie seiner Erweiterungsringe, d.h. die additive Einheit und somit a + 0 = 0 + a = 0.
Die Null ist die erste Catalan-Zahl. Die Null ist auch die einzige komplexe Zahl, die sowohl reell als auch rein imaginär ist.

Im Allgemeinen werden heute die Axiome der natürlichen Zahlen von Peano (1891) angegeben durch:
1. 0 ist eine natürliche Zahl
2. Jede Zahl n hat genau einen Nachfolger n‘
3. 0 ist nicht Nachfolger einer Zahl
4. Jede Zahl ist Nachfolger höchstens einer Zahl
5. (Induktionsaxiom) Von allen Mengen, die die Zahl 0 und mit der Zahl n auch deren Nachfolger n‘ enthalten, ist die Menge N der natürlichen Zahlen die kleinste.

Allerdings sah Peano selbst die 0 nicht als natürliche Zahl. Auf Grund der Entwicklung der Algebra (Gruppen- und Ringtheorie) wird die Null heute zu den natürlichen Zahlen gezählt. Andersartige, immer wieder vorkommende, Veröffentlichungen sind algebraisch nicht begründbar.
Nach dem Werk „Assiomi di Peano“ [da Peano G., Formulario Mathematico, Fratelli Bocca {indicato sul frontespizio come Fratres Bocca} Editore, Torino 1908, pag. 21]) soll Peano „Zero es numero“ formuliert haben.
Bis heute konnte nicht geklärt werden, ob die Null für Peano vielleicht doch die erste natürliche Zahl war.

In dem für die Mathematik fundamentalen Werk „Moderne Algebra“ nennt van der Waerden als erstes Axiom:
1. 1 ist eine natürliche Zahl
und schließt die Null damit aus.

Die Null wird in verschiedenen Sprachen zur Charakterisierung besonderer Umstände genutzt. Im Deutschen bedeutet „Null Komma nichts“ umgangssprachlich absolut nichts.
Im Italienischen wird „a chilometri zero“ (in Null Kilometer Abstand) für „lokal“ verwendet. Zum Beispiel bedeutet „un gelato a chilometri zero“ ein „Eis aus lokaler Produktion“.
Im Taoismus ist „wuji“, die Zahl 0, das mystische Symbol für das Chaos, den Anfang und das Ende.

Zahl 3

Die Dreiteilung eines Winkels war eines der drei klassischen Probleme der Antike, neben der Quadratur des Kreises und der Verdopplung des Würfels. Es gibt drei Parkettierungen der Ebene durch regelmäßige Vielecke: das gleichseitige Dreieck, das Quadrat und das regelmäßige Sechseck der Bienenwaben.

Drei teilt alle Zahlen, die um eins kleiner sind als eine Potenz von zehn, auch, wenn die aus ihren Ziffern gebildete Quersumme durch drei teilbar ist. Jede genügend große ungerade Zahl ist die Summe von höchstens drei Primzahlen. 3 ist 1!+2!. Das kleinste magische Quadrat hat die Kantenlänge 3.
3 ist die höchste Zahl in der Sprache des Yankos-Stammes am Amazonas: „Poettarrarorincoaroac“.
Die Erde ist der dritte Planet in unserem Sonnensystem.

In der christlichen Mythologie ist die 3 eine der wichtigsten Zahlen überhaupt, insbesondere im Blick auf die Dreieinigkeit Gottes. Während Halos auf mittelalterlichen Gemälden meist kreisförmig sind, wird das Dreieck daher ausschließlich für Gott verwendet.

Weiterhin findet man in der Bibel den dreifachen Segen des Aaron (Num 6,24-26), die Dreizahl der hohen Feste (Ex 23,24), die Dreimaligkeit des täglichen Gebets (Dan 6,11), im dreifachen Opfer, aber auch die Heiligen Drei Könige (Matth 2,1), die drei Jünger Petrus, Jakobus und Johannes (Mt 26,37-45), die dreifache Verleugnung Jesu durch Petrus (Joh 13,38), usw. Allerdings wurde Jesus auch dreimal vom Teufel versucht (Mt 4,1-11). Das Tier in der Apokalypse ist dreigestaltig. Die Dreigestaltigkeit findet sich auch in den Begriffen: Mann, Frau und Kind; Beginn, Mitte und Ende; Geburt, Leben und Tod.

Die frühere Anschauung der Vollkommenheit der 3 zeigt sich auch in dem Sprichwort „Aller guten Dinge sind Drei“. Auch in Märchen findet sich die 3: z.B. drei Wünsche, die man frei hat, drei Mordversuche an Schneewittchen, drei Prüfungen für die Goldmarie, Zaubersprüche müssen dreimal aufgesagt werden, drei Besuche von Rumpelstilzchen, drei Schwestern in Aschenputtel (von denen aber nur eine fleißig ist), die Märchen von den 3 kleinen Schweinchen oder vom „Teufel mit den drei goldenen Haaren“, am „dritten Brünnlein“ wird das Brüderchen zum Reh, usw.
3 Personen werden auch gern als Comic-Helden genommen, z.B. Tick, Trick und Track in den „Duck-Tales“, Dig, Dag und Digedag im „Mosaik“ oder Colt, Rocky und Tum Tum, die 3 Ninjas.

Durch Plato werden in „Republik“ drei Schicksale beschrieben, die Parzen oder Töchter der Notwendigkeit. Diese teilten allen Menschen bei der Geburt ihren Anteil an Glück und Unglück zu.
In der Kunst werden sie als strenge alte Frauen oder als düstere Jungfrauen dargestellt. Klotho, die Spinnerin, flocht den Lebensfaden. Lachesis, die Lose-Zuteilerin, maß ihn und wies jedem Menschen sein Schicksal zu. Atropos, die Unabwendbare, trug die furchtbare Schere, mit der sie den Lebensfaden zur gegebenen Zeit abschnitt. Die Entscheidungen der Parzen konnten nicht geändert werden, selbst von den Göttern nicht.

In der griechischen Mythologie kennt man auch drei Sirenen, die u.a. Odyseus auf seiner Irrfahrt traf. In Shakespeares Macbeth treten drei Hexen auf.
Man kennt auch die 3 Furien. In der griechischen Mythologie werden sie die Erinyen genannt (griech: ErinueV). Die Erinyen sind eine Gruppe von Rachegöttinnen des Mutterrechts: Alekto, „die Unaufhörliche“, Megaira, „der neidische Zorn“ und Tisiphone, „die Vergeltung“.

Ebenso bekannt ist das Urteil des Paris, der von den Göttinnen Hera, Athene und Aphrodite die schönste wählen sollte; mit einem schrecklichen Ende für Troja.
Prometheus („der vorher Denkende“) warnte seinen Bruder Epimetheus („der hinterher Denkende“). Dennoch nahm dieser Pandora zur Frau. Diese öffnete ihre Brüchse und zwei der drei Dinge wurden frei, Elend und Krankheit. Nur die Hoffnung blieb in der Büchse.

Captain Kirk und Spock spielten in Star Trek 3 Partien Schach und Kirk gewann alle! Zu einer Skat-Partie gehören mindestens 3 Spieler.
Nicola Tesla war von der 3 absolut fasziniert. Er umrundete jedes Gebäude erst dreimal, bevor er es betrat.
Oktopusse haben 3 Herzen. Skat wird mit mindestens 3 Personen gespielt.

Der Satz von Winogradow sagt aus, dass jede hinreichend große ungerade Zahl die Summe von 3 Primzahlen ist.
Der indische Mathematiker Srinivasa Ramanujan (1887-1920) fand die Beziehung √(1 + √(1 + 2 √(1 + 3 √(1 + 4 √(1 + …))))) = 3.

Besitzt Weiß auf einem Schachbrett alle Figuren in Ausgangsstellung und Schwarz nur den König auf h4, dann benötigt Weiß nur 3 Züge bis zum Matt. siehe 337.Schachproblem im »Problemschach
Die möglichen Zugfolgen sind
d2-d4 , Kh4-g4 , e2-e4 , Kg4-h4 , g2-g3 Matt
d2-d4 , Kh4-h5 , Dd1-d3 , Kh5-g4 , Dd3-h3 Matt
d2-d4 , Kh4-h5 , Dd1-d3 , Kh5-h4 , Dd3-h3 Matt
Steht der einzelne schwarze König auf den Feldern h5, h6 oder g4, so benötigt man 6 Züge zum Matt (Schachprobleme 338 bis 340).
3 ist die Anzahl der Primärfarben (Rot, Grün, Blau) ud ebenso die Anzahl der Grundfarben bei subtraktiver Farbmischung (Cyan, Magenta, Gelb).

Die Zahl 3 als Wertstufe einer Banknote ist ziemlich selten. Zu finden ist sie aber auf der kubanischen 3-Peso-Note mit dem Bildnis von Ernesto Che Guevara.

Abbildung: kubanische 3-Peso-Note

In Dimensionen ab der 5. existieren immer nur genau 3 regelmäßige Polytope. In der Farbenlehre werden 3 additive Farben (rot, grün, blau) und 3 subtraktive Farben (cyan, magenta, gelb) betrachtet.
NUMB3RS ist die erfolgreichste US-amerikanische Fernsehserie, in der Mathematiker Hauptrollen spielen.
weitere Eigenschaften der „3“ siehe http://primes.utm.edu/curios/page.php/3.html .

Zahl 13

Die 13 ist Wilson-Primzahl und kleinste Mirp-Zahl. In der Stereometrie sind genau 13 halbreguläre Polyeder, die Archimedischen Körper, bekannt.
Die 13 ist die kleinste Zahl des ersten Heronischen Zahltripels (13, 14, 15). 13 ist auch die Hypotenusenlänge im zweitkleinsten primitiven pythagoreischen Tripel (5, 12, 13).
13² = 169 und 31² = 961
π(13) = 1! 3!

Auf der US-amerikanischen 1-Dollar-Banknote ist ein Olivenzweig mit 13 Blättern abgebildet. Über dem Adler-Kopf findet man auch 13 Sterne, die für die 13 Gründerstaaten der USA stehen.
Die US-amerikanische Flagge hat ebenso 13 Sterne und 13 Streifen.
Durch den jüdischen Gelehrten Mosche ben Maimon (Maimonides 1134-1204) wurden 13 Glaubensgrundsätze verfasst.

Darüber hinaus gilt die 13 in der Bevölkerung als „Unglückszahl“, obwohl die 13 die 5.glückliche Zahl ist. Einer Allensbach-Umfrage aus dem Frühjahr 2005 zufolge fürchten 28(!!!) Prozent der Deutschen diese Zahl; im 21.Jahrhundert! Triskaidekaphobia heißt die „Angst vor der 13“. Diese unheilvolle Bedeutung kam endgültig auf, als im Christentum die 13 mit dem letzten Abendmahl in Verbindung gebracht wurde.

Das Jahr umfasst 13 x 4 Wochen. Im Kartenspiel gibt es 13 Karten einer Farbe.
Die Babylonier begegneten der 13 mit Misstrauen. Der 13. als Schaltmonat eingeführte Monat galt als Unglücksmonat. Diesem wurde das Sternbild Rabe zugeordnet. Seit dieser Zeit gilt der Rabe als Unglücksvogel.
In der nordischen Mythologie führte ein Festessen in Walhalla mit 13 Gästen zum Tode von Baldur.

Ende des 19.Jahrhunderts wurde in Paris die Hausnummer 13 nicht benutzt, in London benutzte man als Ersatz die Nummer 12A. Im Hotel Carlton Tower gelangte man 1960 vom 12.Stock sofort in den vierzehnten. (siehe Abbildung)
In Italien wird bei Lotteriescheinen die 13 weggelassen. Im John Hopkins Hospital in Baltimore gibt es keinen Operationssaal mit der Nummer 13.

Bei der Reise der englischen Königin 1965 durch Deutschland wäre ihr Zug in Duisburg am Bahnsteig 13 angekommen. Kurzerhand wurde er in 12A umbenannt.
Als Prinzessin Margaret 1930 auf Glamis Castle in Schottland geboren wurde, registrierten die Hofbeamten die Geburt erst einige Tage später. Andernfalls hätte sie die Nummer 13 bekommen.
In der christlichen Mythologie wird die 13 ebenfalls als Unglückszahl gesehen. Vor dem Tod Jesu nahmen am österlichen Abendmahl 13 Personen teil, von denen Judas für 30 Silberlinge Jesus verriet. Seitdem bittet man ungern 13 Personen zu Tisch. In Frankreich gab es eine Gruppe von Adligen, die kurzfristig irgendwelche Anlässe retteten, bei denen nur 13 Gäste erschienen waren.

Alle „Zahl 13“-Fanatiker erhielten 1970 neue Nahrung. Ausgerechnet „Apollo 13“ wurde auf Grund eines Unfalls fast zur Katastrophe. Die Explosion der Sauerstofftanks fand übrigens am 13.(!)April statt und die Mondlandefähre hieß „Odyssee“.
Der Start der Apollo 13-Mission erfolgte übrigens 13 Uhr 13 Minuten amerikanischer Zentralzeit von Rampe 39 (= 3·13). Drei der Schlafperioden der Astronauten begannen 13 Minuten nach der vollen Stunde. Ebenso sollten sie auf dem Mond 13 Minuten nach einer vollen Stunde landen. Bei diesem Thema kommen die Zahlenmystiker voll auf ihre Kosten.

Im Judentum dagegen wird das Erreichen des Alters von 13 Jahren eines Jungen (Bar Mizwa) als großes Ereignis gefeiert. Entsprechend eines reaktionären Frauenbildes gibt es etwas ähnliches für jüdische orthodoxe Mädchen nicht.

Philipp von Makedonien trug in seinen Prozessionen stets 12 Götterbilder. Als er sich selbst in Gold modellieren ließ und somit 13 Bilder mit sich führte, wurde er von einem Hauptmann seiner Leibgarde ermordet.
In der nordischen Mythologie gesellte sich der dämonische Loki zum Festmahl der Götter. Er brachte Zwietracht und führte direkt zum Tod Balders, dem Gott des Lichtes.

Kombinationen von 13 Personen, d.h. 12 + 1 hervorgehobenen, findet man eine Vielzahl: zuerst Jesus und seine Jünger, Robin Hood und seine Gesellen, König Artus und die Ritter der Tafelrunde, der skandinavische Anführer Rollo und seine Krieger, usw…

Extrem wird der Aberglaube, wenn im Kalender ein 13. eines Monats zusätzlich noch auf einen Freitag fällt. Mindestens einmal und höchstens drei Mal tritt ein derartiger Tag im Jahr ein.
Der 13.Mai 2011 war sogar ein „doppelter“ Freitag, der 13. Addiert man die Ziffern des Datums ergibt sich wieder 13. Der nächste derart schreckliche Tag ist der 13.Januar 2141.
Übrigens wurde die Zahl 13 in der Geschichte des deutschen Lottos von 1955 bis 2003 von allen Zahlen am wenigsten gezogen!

Zahl 14

14 und 15 sind das erste Paar aufeinanderfolgender Zahlen, deren Summe ihrer Teiler, die Zahlen selbst eingeschlossen, gleich sind: 1+2+7+14=1+3+5+15=24
14 ist die Anzahl der Bravais-Gitter und die kleinste gerade natürliche Zahl, die nicht als Funktionswert der Eulerschen φ-Funktion auftritt.
Genau 14 Brüche benötigt Conway für sein Primzahlsieb, mit dem alle(!) Primzahlen in der korrekten Reihenfolge berechnet werden können.
Es gibt keine Zahl, die 14 zur ihr relativ prime und kleinere Zahlen besitzt. 14 ist die kleinste Keith-Zahl.
Die 14 gilt als vorteilhaft. Der Mond benötigt rund 14 Tage vom Vollmond zu Neumond. Daraus resultiert die gebräuchliche Zeitangabe 14 Tage.

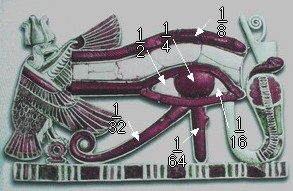Der ägyptische Gott Osiris wurde als Auge am Ende einer 14stufigen Treppe dargestellt. (Abbildung) Sein Bruder Set tötete ihn und schnitt ihn dann in 14 Teile.

In der jüdischen Mythologie kommt der 14 eine besondere Stellung zu, da das Passah-Fest am 14.Nissan gefeiert wird. Frühe Christen und spätere christliche Anhänger eines christlichen Ostertermins ebenfalls am 14.Nissan wurden „Quartodecimaner“ („die Vierzehner“) genannt.

Im Evangelium des Matthäus heißt es weiter:
„Alle Glieder von Abraham bis auf David sind vierzehn Glieder. Von David bis auf die babylonische Gefangenschaft sind vierzehn Glieder. Von der babylonischen Gefangenschaft bis auf Christum sind vierzehn Glieder.“
Zählt man wirklich nach, so stellt man fest, das es nicht stimmt.
Es werden 14 Stationen des Kreuzwegs angegeben. Die katholische Kirche kennt 14 Nothelfer.

Der griechischen Göttin Hera dienten vierzehn Gefährtinnen, von denen ihre Botin Iris am bekanntesten ist. Amphion und Niobe hatten vierzehn Kinder, sieben Töchter und sieben Söhne, die von Apollon und Artemis getötet wurden.
Julia verliebt sich in Shakespeares „Romeo und Julia“ mit 14 Jahren in den sechzehnjährigen Romeo. Ihre Mutter war 14, als sie Julia gebar. Heute würde man das Werk wohl nicht mehr veröffentlichen und der Autor würde sehr viel Ärger bekommen.

Das arabische Alphabet mit 28 Buchstaben unterteilt diese in 14 Sonnen- und 14 Mondbuchstaben.
Die 14 ist die chinesische Unglückszahl, da sie wie „Der sichere Tod“ (ohne Entkommen) ausgesprochen wird.
Es existieren genau 14 Primzahlknoten bis zur Ordnung 7. Die 14 ist auch Catalan-Zahl und quadratische Pyramidenzahl
14 = 1 + 4 + 9 = 1² + 2² + 3².
10¹⁴ – (2 x 14 – 1) und 10¹⁴ – (2 x 14 + 1) sind Primzahlzwillinge.

14 = 2 + 3 + 4 + 5 = 2¹ + 2² + 2³ = (log₂128) (log₇49)
14² – 7² = (14 + 7) x 7

Das Reziproke 1/14 = 0,0714285714285714285… enthält als erste Ziffern 7, 14 und 28, d.h. Faktoren und Vielfache von 14.
Das Kubokateder, der abgestumpfte Würfel und das abgestumpfte Tetraeder sind Polyeder mit 14 Seitenflächen. Das finnische Wort „pääjääjää“ wird mit 14 Punkten geschrieben.
Der französische Sonnenkönig Ludwig der XIV. bestieg den Thron 1643 (Quersumme 14), starb 1715 (Quersumme 14) und regierte 77 Jahre (Quersumme 14).

Zahl 15

15 ist die größte Zahl, für welche die Gleichung 2ⁿ – 7 = x² (n = 15) eine ganzzahlige Lösung für x hat.
15 ist die Anzahl der Archimedischen Körper, wenn nicht-spiegelungsinvariante Körper doppelt gezählt werden. 15 ist die kleinste zusammengesetzte Zahl n, für die bis auf Isomorphie nur eine einzige Gruppe der Ordnung n existiert. Kleinste Pseudoprimzahl.
Kleinste natürliche Zahl, die sich nicht als Summe von weniger als acht Kubikzahlen schreiben lässt (Waring-Problem).
15 ist die fünfte Dreieckszahl: 15 = 1 + 2 + 3 + 4 + 5.
15 = 3 log₂ 32 = 4! + !4 (subfaktorial) = 8² – 7² = 4² – 1².
2^4n-1 und 3n⁵ + 5n³ + 7n sind für alle natürlichen n durch 15 teilbar.
15² = (1 + 2)(3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12)
15⁴ = 4⁴ + 6⁴ + 8⁴ + 9⁴ + 14⁴

15 ist die erste Zahl gleich dem Produkt zweier verschiedener, ungerader Primzahlen.
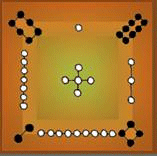
Die Summe der Zeilen, Spalten und Diagonalen des kleinsten magischen Quadrates ist 15 (siehe Abbildung). Das Pool-Billiard hat fünfzehn Kugeln im Dreieck.

15 und 21 sind das erste Paar von Dreieckszahlen, deren Summe und Differenz (6/36) wieder Dreieckszahlen sind. Das nächste kommt erst bei 780 / 990, dann erst bei 1 747 515 / 2 185 095.
In Mel Brooks „Verrückten Geschichte der Welt“ erhält Moses 15 Gebote von Gott. Da Moses aber eine der drei Tafeln fallen lässt, sind es nur noch 10 Gebote. Bei „Lara Croft: Tomb Raider“ erfährt man, dass der 15. niemals ein „guter Tag“ ist.
Da die 10 in der hebräischen Kabbalistik dem Buchstaben J und die 5 einem H entspricht und beide zusammen Teile des Namens Gottes (Jahwe) sind, wird von Juden vermieden, die 15 zu schreiben und stattdessen 9+6 benutzt. Den Namen Gottes zu schreiben, ist im Judentum ein Tabu.
Das Volk der Huli im südlichen Hochland von Papua-Neuguinea verwendet ein Zahlensystem auf der Basis 15. Zum Beispiel sagen die Huli für „93“: ngui waraga, ngui kane-gonaga tebira. Dies bedeutet „15 mal 6 + 3 Objekte der siebenten 15“.

Zahl 17

17 ist die siebente Primzahl, dritte Fermat-Primzahl und ebenso Mersennesche Primzahl; verbunden mit der 6.vollkommenen Zahl 8589869056.

Im Alter von 17 Jahren bewies Gauß, dass man ein reguläres Polygon nur dann mit Zirkel und Lineal konstruieren kann, wenn diessen Seitenzahl gleich einem Produkt aus lauter verschiedenen Fermatschen Primzahlen der Form 2^2^n +1 ist. Daraus folgt, dass man das reguläre Siebzehneck mit Zirkel und Lineal konstruieren kann. Gauß hielt die Konstruktion des regelmäßigen 17-Ecks mit Zirkel und Lineal für eine seiner wichtigsten Entdeckungen.
Auf dem Sockel des Gauß-Denkmals in Braunschweig sieht man einen Stern in einem regelmäßigen Siebzehneck (Abbildung).

17 ist die einzige Primzahl, welche sich als Summe vier aufeinanderfolgender Primzahlen darstellen lässt: 17 = 2 + 3 + 5 + 7.
17 ist die kleinste Zahl, für welche die Summe der Ziffern ihrer Kubikzahl gleich der Zahl selbst ist: 17³ = 4913, 4 + 9 + 1 + 3 = 17. (Die größte derartige Zahl ist 27)
17 ist ebenso die kleinste Zahl, welche auf zwei verschiedene Arten als Summe eines Quadrates und einer Kubikzahl dargestellt werden kann: 17 = 3² + 2³ = 4² + 1³. Außerdem ist 17 die einzige Primzahl der Form pq + qp, mit primen p und q, p = 2, q = 3.
Das Paar (8, 9) ist das einzige Paar aufeinanderfolgender Zahlen, von denen eine Quadrat und eine Kubus ist (Beweis durch Euler).
Der Term n² + n + 17 ist für alle n = 0 bis 15 Primzahl. Weiterhin ist
17 x 65 359 477 124 183 = 1 111 111 111 111 111
17² = 8² + 15² (pythagoreisches Tripel) = 1³ + 2³ + 4³ + 6³ = 0⁰ + 1¹ + 2² + 3³ + 4⁴
17⁴ = 83521 = (8 + 3 + 5 + 2 – 1)⁴
17⁶ = 24137569 = (24 – 13 + 75 – 69)⁶
Zahlen der Form abcdefghabcdefgh sind durch 17 teilbar, da 100000001 ein Vielfaches von 17 ist.

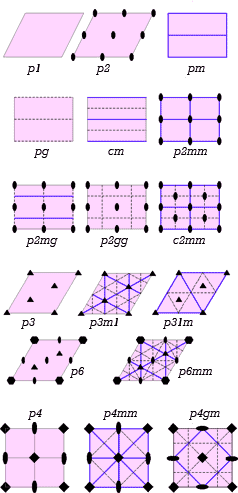Weiterhin existieren genau 17 ebene Kristallgruppen, d.h. Ornamentgruppen (engl. wallpaper groups)
In der Alhambra findet man 17 verschiedene Parkettarten, d.h. alle möglichen.
Abbildung: Ornamentgruppen

Die 17 ist eine „psychologische“ Zahl. Fordert man Leute auf, eine beliebige Zahl zwischen 1 und 20 zu nennen, wird die 17 überdurchschnittlich oft genannt.
Sehr beliebt sind psychologische Zahlen bei Schriftstellern aber auch in Filmen. Wird eine etwas größere Zahl benötigt, der allerdings keine besondere Bedeutung beigemessen werden soll (z.B. die 13 als „Unglückszahl“), verwendet man gern diese Zahlen, darunter sehr oft die 17.

Ein Hyperwürfel muss entlang von 17 Flächen zerschnitten werden um in ein dreidimensionales Kreuz zu zerfallen.
Im orientalischen Kamelproblem treten 17 Kamele auf. In der japanischen Gedichtform Haiku werden 17 Silben verwendet.

Die Pythagoräer hatten; nach Plutarch; Angst vor der 17, weil sie zwischen 16 und 18 liegt, die die einzigen Werte sind, für die der Umfang eines Rechtecks gleich dessen Fläche ist.
In Frankreich und vor allem Italien bringt Freitag der 17. Unglück, so entschloss sich einst Napoleon seinen Staatsstreich vom 17. auf den 18.Brumaire der Jahres 1799 zu verschieben.
Die italienische Fluggesellschaft Alitalia hat in ihren Flugzeugen keine Reihe 17, italienische Gebäude haben kein 17.Stockwerk, in Hotels wird das Zimmer 17 mit 16bis bezeichnet. Es wurde niemals ein Renault 17 verkauft – er wurde zu 117 umgetauft!
Der Grund für die Ablehnung der 17 stammt aus dem Latein. Die Zahl XVII kann in VIXI umsortiert werden, was „verstorben“ bedeutet.
Die Angst vor der 17 wird Heptadekaphobie bzw. Heptakaidekaphobie genannt.

In den USA leben Singzikaden, die sich nur alle 13 oder 17 Jahre paaren. Beispielsweise verlässt die Siebzehnjahr-Zikade (Magicicada septendecim. Abbildung) erst nach genau 17 Jahren ihr unterirdisches Versteck, um sich in einem Zeitraum von etwa drei Wochen zu vermehren.

Die mystische Bedeutung der Zahl 17 findet man u.a. in der Bibel. Am 17.Tag des 2.Monats begann die Sintflut und endete am 17.Tag des siebenten Monats. Es ist 2² + 3² + 5² + 7² + 11² + 13² + 17² = 666, die „Zahl des Tieres“.
Odysseus trieb 17 Tage auf einem Floß, nachdem er Kalypso verlassen hatte. Der persische Prophet Zarathustra verfasste in den „Gatahs“ 17 visionäre Hymnen.

Mit Trick 17 beschreibt man Lösungswege bei Problemen, die originell, speziell oder einfach nur verblüffend sind. In der Schweiz sagt man aber Trick 77.
17 als Alter kurz vor der Volljährigkeit ist in Schlagern der Nachkriegszeit das symbolische Alter beinah erwachsener Mädchen und findet sich in Titeln wie „Mit 17 hat man noch Träume“, „Siebzehn Jahr, blondes Haar“ und ähnlichen „Werken“. Der Beatles-Titel „I saw her standing there“ hieß ursprünglich „Seventeen“.
Bei einem Lächeln werden 17 Muskeln bewegt. 🙂 17 ist die kleinste natürliche Zahl, die im Französischen mit einem Bindestrich geschrieben wird: dix-sept.

Im Papyrus Rhind findet sich die Zerlegung 2/17 = 1/2 + 1/51 + 1/68, die allerdings falsch ist, der einzige(!) Fehler in diesem historischen Text.
17 ist die einzige Primzahl, die das arithmetische Mittel zweier aufeinanderfolgender Fibonacci-Zahlen (13 und 21) ist. Keine ungerade Fibonacci-Zahl ist durch 17 teilbar.

Der pflanzenfressende Stegosaurier (Stegosaurus armatus) hatte 17 Schildplatten auf dem Rücken und lebte etwa vor 157 bis 147 Millionen Jahre.
Heute sind nur noch 17 Originalkopien der Magna Carta bekannt.
Der Parthenon auf der Akropolis hat 8 Säulen in der Breite, aber 17 Säulen auf der längeren Seite.

Im 5.Jahrhundert v.u.Z. bewies Theodorus von Kyrene, dass alle Quadratwurzeln aus den ungeraden Primzahlen bis 17 irrational sind. Warum er bei 17 aufhörte, ist nicht bekannt.
Man vermutet, dass in einem klassischen Sudoku mindestens 17 Zahlen gegeben sein müssen, um eine eindeutige Lösung zu gewährleisten. 2009 ist dies noch nicht bewiesen.
Es gibt 17 verschiedene Standardformen der quadratischen Quadriken.

Zahl 42

„… is the ultimative answer to life, the universe, and everything,“
The hitchiker’s guide to the galaxy, Adams

Die 42 ist die „Kultzahl“ schlechthin!
In dem skurrilen Buch „Per Anhalter durch die Galaxie“ ist 42 die Antwort auf die“ultimativ letzte Antwort zum Leben, zum Weltall und allen anderen Dingen“.

Allerdings kennt der Autor Douglas Noel Adams (DNA !) vorerst die zugehörige Frage nicht.
Im Nachfolgeband „Das Restaurant am Ende des Universums“ beschließt Douglas das Kapitel 33 mit dem Ergebnis:
„Das ist es. – Neun mal sechs. Zweiundvierzig – Das ist es. Das ist alles.“

Das Ergebnis ist zwar nicht 42, aber was macht das schon.
In der Handlung dieses Science-Fiction-Klassikers wurde der Computer Deep Thought damit beauftragt, die Antwort zu errechnen. Nach 7,5 Millionen Jahren gab Deep Thought die Antwort „Zweiundvierzig“ sowie den Hinweis, dass die Erklärung dieser Antwort sich ergibt, wenn die eigentliche Frage erst hinreichend formuliert sei.

Da die im zweiten Teil gefundene Frage nach herkömmlicher Arithmetik nicht richtig ist, führt es unter anderem zur Feststellung, dass das Universum keinen Sinn ergibt.

Anmerkung: die Formel „neun multipliziert mit sechs“ würde nur in einem 13er-Stellenwertsystem 42 ergeben: 4·13 + 2·1 = 54 = 9·6. Im Dualsystem lautet die Ziffernfolge von 42 gerade 101010.
Douglas Adams schrieb in einem Usenet-Beitrag 1993 auf die Frage warum die Antwort „42“ sei:

„Die Antwort darauf ist ganz einfach. Es war ein Scherz. Es musste eine Zahl sein, eine normale, kleine Zahl, und ich wählte diese. Binäre Darstellungen, Basis 13, Tibetanische Mönche, das ist alles kompletter Unsinn. Ich saß an meinem Schreibtisch, sah in den Garten und dachte ’42 geht‘. Ich schrieb es. Ende der Geschichte.“

Im antiken Ägypten glaubte man, dass das Schicksal von Toten von 42 Dämonen entschieden werde. Der Verstorbene musste diesen 42 Göttern eine Frage wahrheitsgemäß mit „Nein“ beantworten. Nur dann galt er als gerecht. Die Hindus verehrten eine Gottheit mit 42 Armen.

Ähnlich wie Douglas Adams hatte auch Lewis Carroll eine Vorliebe für die 42.
In „Alice im Wunderland“ kommt die „Regel 42“ (Alle Leute, die größer als eine Meile sind, müssen den Hof verlassen) vor, ohne die Regeln 1 bis 41 zu nennen.

„Rule Forty-two. ALL PERSONS MORE THAN A MILE HIGH TO LEAVE THE COURT.“

In der deutschen Synchronisation des Disney-Trickfilms wird von einer Regel 51 statt 42 gesprochen. Warum eigentlich?
Im Vorwort von „Die Jagd nach dem Schnark“ nennt Carroll eine weitere Regel 42.

Unter der Newsgroup alt.fan.douglas-adams findet man im Internet ein „Gedicht“ zur Ehren Douglas Adams, frei nach „Let it be“ der Beatles:

When I find myself in times of trouble,
            Douglas Adams comes in view
            Speaking words of wisdom: «Forty-two.»
            And in my hour of darkness,
            He is the light that shines on through
            Speaking words of wisdom: «Forty-two.»
            Forty-two, forty-two, forty-two, forty-two.
            Whisper words of wisdom: forty-two.
            What are the broken-hearted People
            Living in the world to do?
            There will be an answer: Forty-two.
            For though they may be parted,
            There is still a chance to see what’s true.
            There will be an answer: forty-two.
            Forty-two, forty-two, forty-two, forty-two.
            There will be an answer: forty-two.

In der US-amerikanischen Fernsehserie „Lost“ tritt ständig eine Zahlenfolge auf: 4, 8, 15, 16, 23 und 42(!). Ohne die 42 geht es wohl nicht mehr.

42 ist die magische Konstante des kleinsten magischen Würfels, der die Zahlen zwischen 1 und 27 enthält. Die Anzahl der Partitionen der 10 ist ebenfalls 42 (nach Beyer 2017).
42 ist abundant, Catalan-Zahl, Reziprokes einer Bernoulli-Zahl, Størmer-Zahl und die zweite sphenische Zahl. 42 ist auch das Produkt der ersten drei Glieder der Sylvester-Folge. Außerdem ist die 42 Selbstzahl und Harshad-Zahl.

Verwirrend ist, dass man mittlerweile weiß, dass die 42 auch mit der Riemannschen Vermutung verbunden ist.
Die ersten „Momente“ der Riemannschen Zeta-Funktion sind 1, 2, 42(!), 24024.

1/T 0∫T | ζ(1/2 + it) |6 dt ∼ 42/9! Πp (1 – 1/p)4 (1 + 4/p + 1/p²) log9 T

In dem Term wird das Produkt über alle Primzahlen gebildet.
Durch Jon Keating wurde außerdem eine Formel des Quantenchaos gefunden, die gerade diese Momente berechnet, d.h. also auch die 42!

42 ist auch die Höchstpunktzahl eines Teilnehmers der internationalen Mathematikolympiade.
Ein Regenbogen erscheint bei einer Reflexion unter einem Winkel von 42°. Eines der interessantesten Objekte in unserer Milchstraße, der Orionnebel, hat im Messier-Katalog die Nummer 42.
Und im Januar 2005 wurde dem 42. im Jahr 2001 gefundene Asteroid 2001 DA42 ein Name gegeben; natürlich DouglasAdams!

Das erste gedruckte Buch, die Gutenberg-Bibel, hatte je Seite 42 Zeilen. (Abbildung)
Natürlich kommt die 42 auch in der Bibel vor.
In 2.Könige 2.24 kommen 42 Kinder zu Tode, in 4.Mose 35.6 ist von 42 Städten die Rede, in der Offenbarung mehrfach von 42 Monaten. Das sind 3 1/2 Jahre oder 42·30 = 1260 sogenannte prophetische Tage, gleichwohl bei Daniel von 1 + 2 + 1/2 Jahren und 1290 bzw. 1335 Tagen die Rede ist.

Das Neue Testament beginnt im Matthäus-Evangelium mit dem Stammbaum Jesu, der seit Abraham dreimal 14, also 42 Geschlechter aufweist. Man kommt beim Nachzählen allerdings auf 41 Personen.
Von Abraham bis David sind es 14, von David bis Jesus 28. Auf 42 kommt man, wenn man David zweimal zählt.
Allerdings widerspricht sich die Bibel in Matthäus 1.17, wie üblich, selbst:
Alle Glieder von Abraham bis auf David sind vierzehn Glieder. Von David bis auf die babylonische Gefangenschaft sind vierzehn Glieder. Von der babylonischen Gefangenschaft bis auf Christus sind vierzehn Glieder.
Damit müsste zwischen Josia und Jojachin noch eine Pseudogeneration „babylonische Gefangenschaft“ eingefügt werden.

Nach der Kaballa ist die 42 die Zahl, mit der Gott das Universum schuf.
In der Fernsehserie „The X-Files“ hat Fox Mulders Appartement die Nummer 42. In „Doctor Who“ gibt es eine Episode „42“, die 42 Minuten dauert.
In „Star Trek: The Next Generation“ hat das Raumschiff USS Enterprise (NCC-1701-D) 42 Decks. Das Fabergé-Ei in „James Bond – Octopussy“ hat die Nummer 42.

Die englische Popgruppe „Level 42“ hat sich direkt in Bezug auf Douglas Adams ihren Namen gegeben.
Und natürlich vergessen Numerologen bei irgendwelchen Zahldiskussionen nie die 666:

Es ist 42 = 6·6+6, und 4+2 = 6 ist sogar die Quersumme von 42, also 42 = 6·7 = (4+2)·(4+2+1). Mit den Bezeichnung q(n) für die Quersumme gilt also
q(n) · (q(n)+1) = n
für die Zahl n = 42. Sie ist eine von nur vier Zahlen n = 12, 42, 90, 156 mit dieser Eigenschaft.

42 = 9 + 10 + 11 + 12 = 13 + 14 + 15 = 0!² + 1!² + 2!² + 3!²
= 2(1 + 2 + 3 + 4 + 5 + 6) = 2² + 2² + 3² + 5²

Addiert man anstelle der Multiplikation, so bleibt nur eine Zahl mit q(n) + (q(n)+1) = n, nämlich n = 17. Deshalb und wegen 42 = 7·2·3 und 17 = 7·2+3 soll die Zahl 17 eine privilegierte Partnerschaft zur Zahl 42 haben.

Und wenn dem so ist, sollte 42 · 42 = 1764 nicht vergessen werden. Da sind neben der 17 die 64 Felder des Schachbrettes.
Gegen eine einzelne weiße Dame gibt es maximal 42 Positionen für eine nicht angegriffene schwarze Figur.

Und wer es noch „toller“ mag, der findet auch in der Näherung 3,14 der Zahl π die 42 mit 3 · 14 = 42. Eine Stelle genauer erhält man mit 3,142 schon wieder 42.
An der 50.Milliardsten Dezimalstelle von π steht 042, ebenso an der 50.Milliardsten Stelle von 1/π.
Ist das noch Zufall? 🙂

Zahl 666

Die 666 ist die biblische Nummer des Antichristen (Offenbarung 13:18) und wird als die „Zahl des Tieres“ (Beast-Number) bezeichnet:

„… Hier ist Weisheit! Wer Verstand hat, der überlege die Zahl des Tieres; denn es ist eines Menschen Zahl, und seine Zahl ist sechshundertsechsundsechzig. …“

Die Zahl 666 ist mit der Erwähnung im Neuen Testament ein begehrtes Ziel der Numerologen, mit allen Merkwürdigkeiten und Auswüchsen. In einer antiken griechischen Abschrift (Nestle-Aland, 1994):
„ωδε η σοφια εστιν ο εχων νοuν ψηφισατω τον αριθμον τοu θηριου αριθμος γαρ ανθρωpου εστιν και ο αριθμος αυτου εξακοσιoι εξηκοντα εξ“
Wörtlich übersetzt ergibt sich der oben genannte Spruch.

Wie immer in der Johannesoffenbarung fehlen konkrete Hinweise auf Namen und Orte, sondern sind chiffriert, wie in Kapitel 17,9 Babylon nach kirchlicher Meinung für Rom steht. Damit wird vermutet, dass die Zahl 666 die verschlüsselte Form eines Namens darstellt.
Im 16.Jahrhundert „bewies“ der Protestant Michael Stifel, dass Papst Leo X. der „Antichrist“ ist; der Katholik Petrus Bungus „bewies“ analog, dass Luther aber auch Muhammad (Mahometus) die Antichristen sind. Wen wundert’s!
In der Abbildung ist der „Beweis“ zu sehen, dass der römische Kaiser Nero der Antichrist war.

Außer der Tatsache, dass solche numerologische Spielchen ohnehin Blödsinn sind, wird die Sache noch problematischer, wenn man bedenkt, dass zum Beispiel im Codex Ephraemi Rescriptus nicht von der 666, sondern von 616 die Rede ist. Auch in der auf den Schweizer Reformator Huldrych Zwingli zurückgehenden „Zürcher Bibel“ steht die Zahl 616.
Der Kirchenvater Irenäus von Lyon wusste, dass in vielen Schriften statt der 666 die 616 zu lesen ist. Er(!) entschied, die 616 für einen Schreibfehler zu halten und nicht die 666.
Abbildung: altgriechischer Papyrus mit der 616 an Stelle der 666

Es gilt 666 = 2² + 3² + 5² + 7² +11² +13² +17² und f(666) = 6 · 6 · 6.
Außerdem ist 666 die 36.Dreieckszahl 1 + 2 + 3 + … + 36 = 666, und die größte „Repdigit“-Dreieckszahl.
Addiert man von den Primfaktoren von 666 = 2 . 3 . 3 . 37 deren Ziffern, ergibt sich 18 = 6 + 6 + 6.
Aus der Zahlenfolge 123456789 können zwei Summendarstellungen für 666 gewonnen werden, aus der Folge 987654321 genau eine:
666 = 1 + 2 + 3 + 4 + 567 + 89 = 123 + 456 + 78 + 9 = 9 + 87 + 6 + 543 + 21
Weiterhin ist 666 = 1⁶ – 2⁶ + 3⁶ / In römischen Ziffern kommt jede Ziffer einmal vor: DCLXVI. Und außerdem
666 = 6 + 6 + 6 + 6³ + 6³ + 6³
666 = (6 + 6 + 6) · (6² + 1²)
666 = 6! · (6² + 1²) / (6² + 2²)

Die ersten 144 Dezimalziffern von π – 3 ergeben in der Summe 666 und außerdem 144 = (6 + 6) · (6 + 6). Eine Zahl der Form 2ⁿ, die die Ziffernfolge 666 enthält, heißt apokalyptische Zahl. Hat eine Zahl 666 Ziffern, so wird sie Apocalypse-Zahl genannt.

In Dan Browns „Da Vinci Code“ wird behauptet, die Glaspyramide vor dem Pariser Louvre würde aus 666 Glasteilen bestehen. Das ist literarische Freiheit. In Wirklichkeit sind es 698 Teile.
Weitere Kuriositäten findet man auf verschiedenen Seiten des Internets.
So werden Bill Gates, Sex, Ronald Reagan aber auch Adolf Hitler als Antichristen „bewiesen“. Hitler (er war Katholik!) ist zwar einer der größten Verbrecher aller Zeiten, dennoch sind alle diese mathematischen Rechnereien einfach nur Unfug.

Auch in der Rockmusik wird auf die Zahl 666 angespielt. Beispiele sind
– „The Number of the Beast“ auf dem gleichnamigen Album von Iron Maiden aus dem Jahr 1982
– Aphrodite’s Child veröffentlichte 1972 ein Doppelalbum mit Musik von Vangelis zur Johannesoffenbarung mit dem Titel 666
– Die Band Genesis nimmt in „Supper’s Ready“ auf der LP Foxtrot ebenfalls Bezug auf die Zahl 666 usw. usf.

Der versuchten Verdummung der Menschen durch die auflagenstärkste, sogenannte „Zeitung“ ist kein Ende zu setzen. Natürlich konnte es sich dieses Blatt nicht verkneifen, am 6.6.2006 folgendes zu veröffentlichen:

„6.6.06 – Ist heute ein gefährlicher Tag?
Die unheimlichste Zahlenkombination – heute regiert sie die Welt: Der Kalender rückt auf „666“ (6.6.06), nach altem Glauben die Zahl des Satans. Wie gefährlich wird dieser Tag?
Der Zahlencode stammt aus der Bibel (Offenbarung 13:18):

„Hier ist Weisheit. Wer Verstand hat, der überlege die Zahl des Tieres; denn es ist die Zahl eines Menschen, und seine Zahl ist sechshundertundsechsundsechzig, heißt es da.‘
Doch Numerologe Arndt Aschenbeck (34) gibt Entwarnung: ‚Durch die Jahreszahl 2006 rückt eine 2 zwischen die drei Sechsen. Sie steht für die Harmonie und Liebe, neutralisiert die negative 666. Vor diesem Tag muß keiner Angst haben‘.“

Ausnahmsweise hat dieser selbst ernannte Numerologe recht. Niemand braucht sich vor dem 6.6.6 oder sonst einem Tag zu fürchten, allerdings vor dem, was dieses Blatt, Numerologen, Astrologen usw. in den nächsten Jahren an weiteren Schwachsinnigkeiten noch verbreiten. Außerdem rücken zusätzlich noch zwei Nullen und eine 2 zwischen die drei Sechsen! Aber wahrscheinlich hat der Numerologe noch nicht verstanden, dass auch die Null eine Zahl ist.
Übrigens sollte diese „Zeitung“ endlich einmal die neue Rechtschreibung lernen!

Nebenbei: Der US-amerikanische Präsident Ronald Reagan und seine Frau Nancy änderten ihre Adresse in Kalifornien von 666 St.Cloud Road auf 668 ab! Offenbar können auch abergläubige Menschen Präsident werden.
In Quentin Tarantinos Film „Pulp Fiction“ hatte die mysteriöse Aktentasche die Schlosskombination 666, was sonst. In „Flucht aus L.A.“ schaltet „Snake“ Kurt Russell weltweit alle Elektronik aus, natürlich mit dem Code 666.